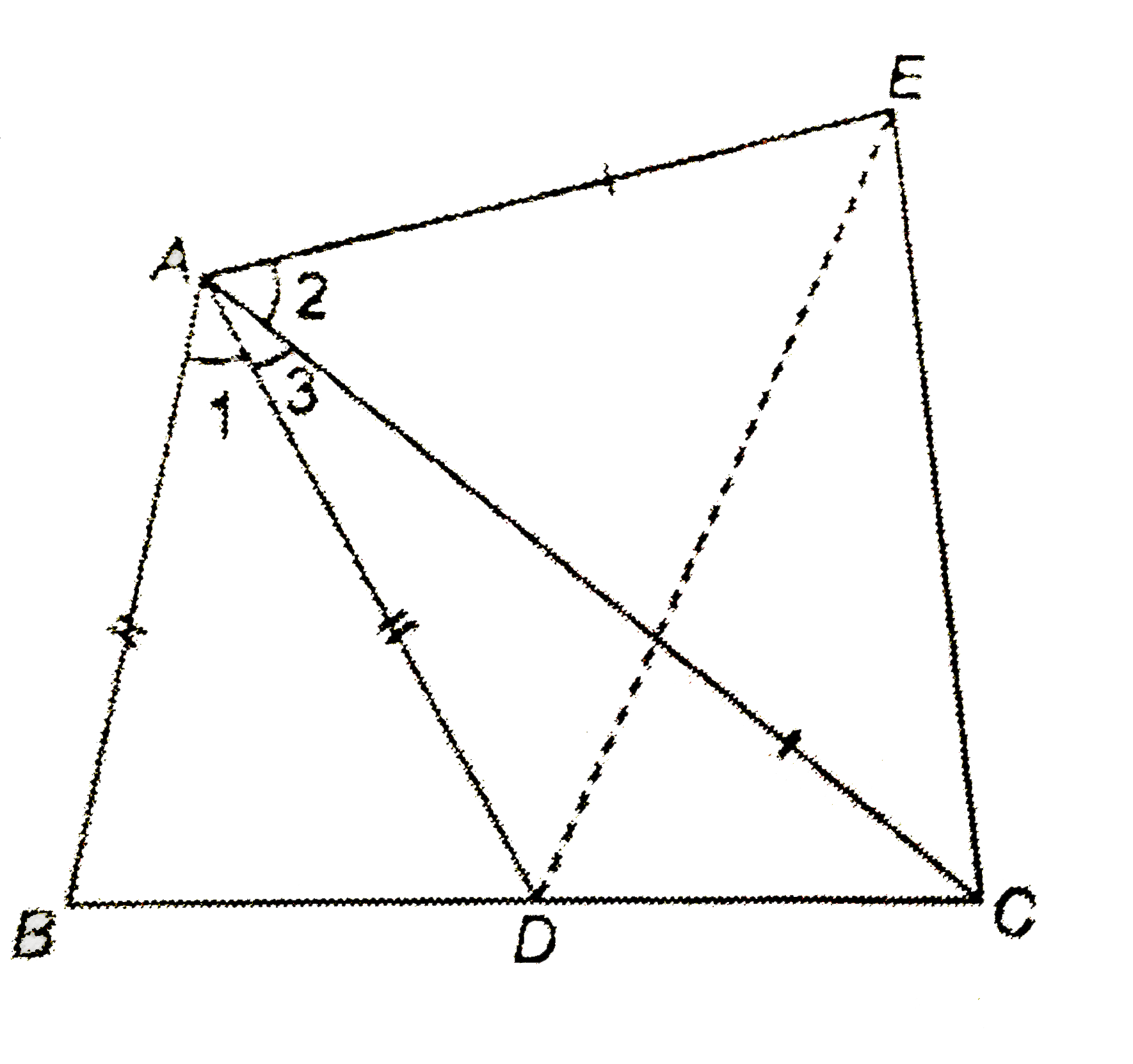
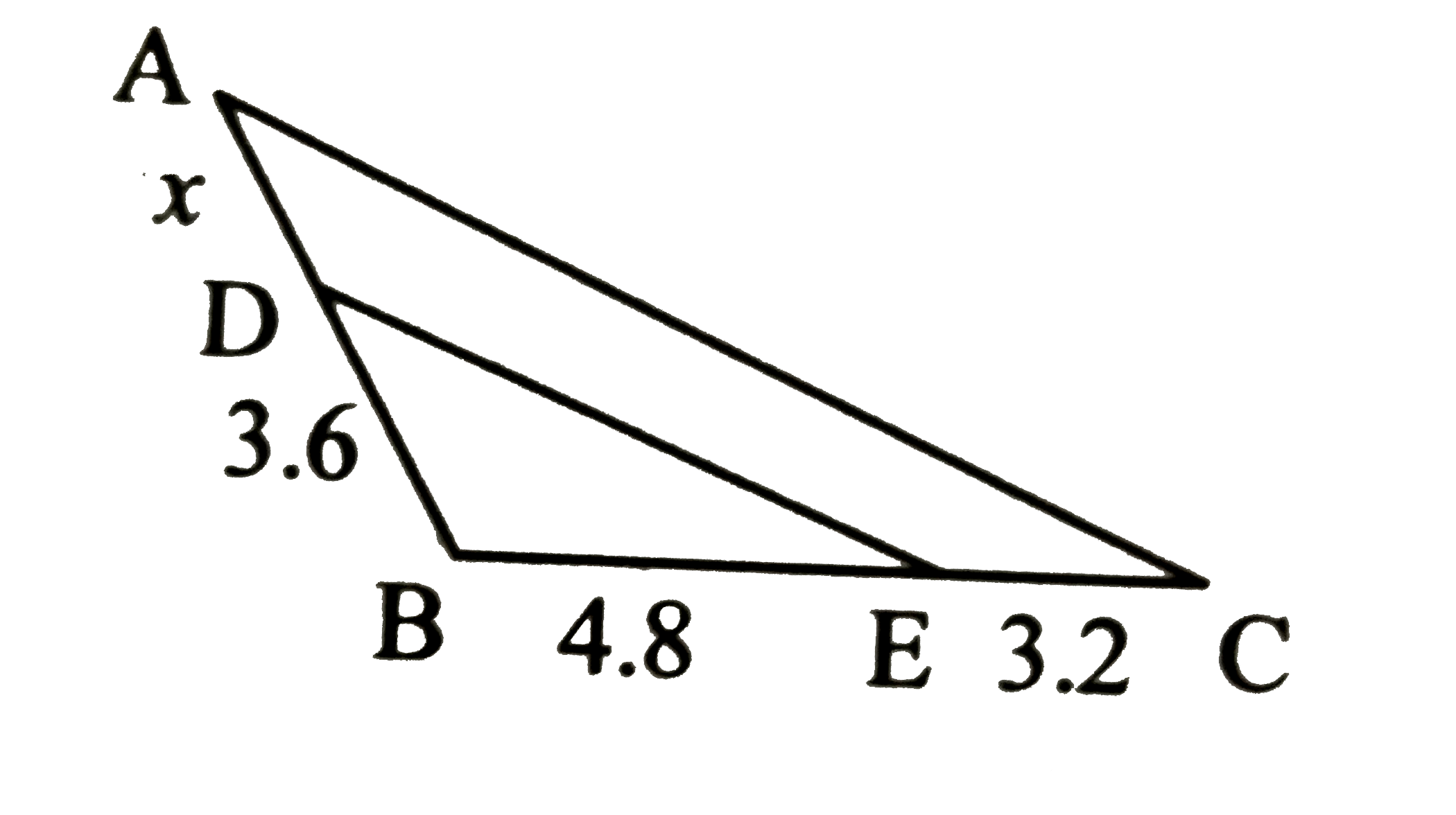In the given figure, in in . Show that .
Video Solution
Text Solution
GIVEN in which AB = AD, AC = AE and
TO PROVE BC = DE.
PROOF In we have
Hence,
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
In the given figure AD=BC,AC=BD. Then ΔPAB is
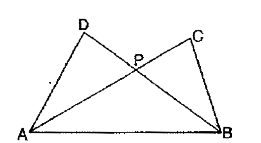 AequilateralBright angledCscaleneDisosceles
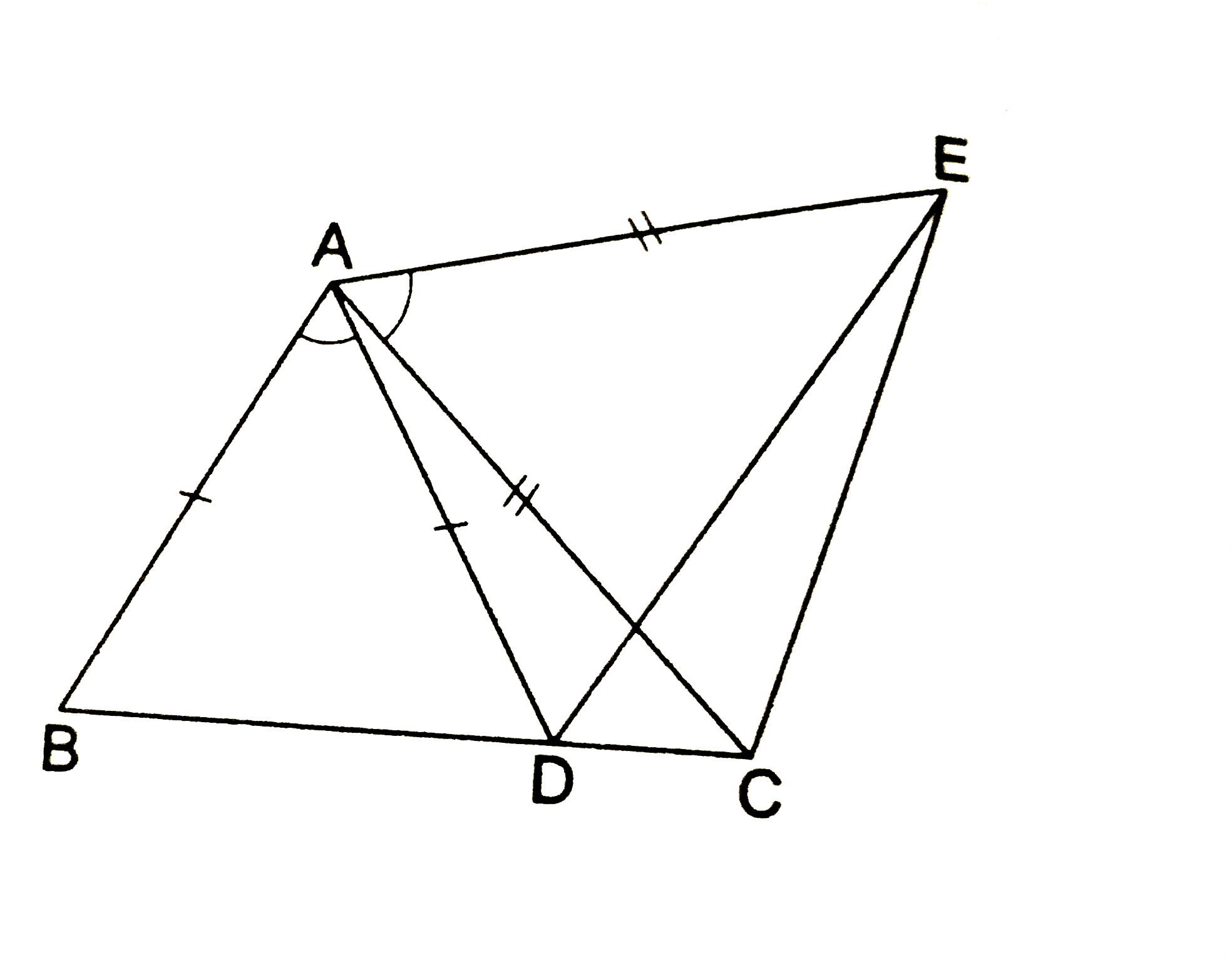
AequilateralBright angledCscaleneDisoscelesIn the given figure, AB = AC and AD = AE. Identify the incorrect statement.
 A∠CAE=∠BADBΔACE≅ΔABDC3CE=EDDBE=DC
A∠CAE=∠BADBΔACE≅ΔABDC3CE=EDDBE=DC
In the given figure, AB = AC and AD = AE. Prove that:
ΔABD≅ΔACE
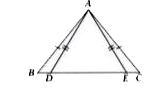
View SolutionIn the given figure, AB = AC and ∠B=∠C.
Then ΔABD≅ΔACE by
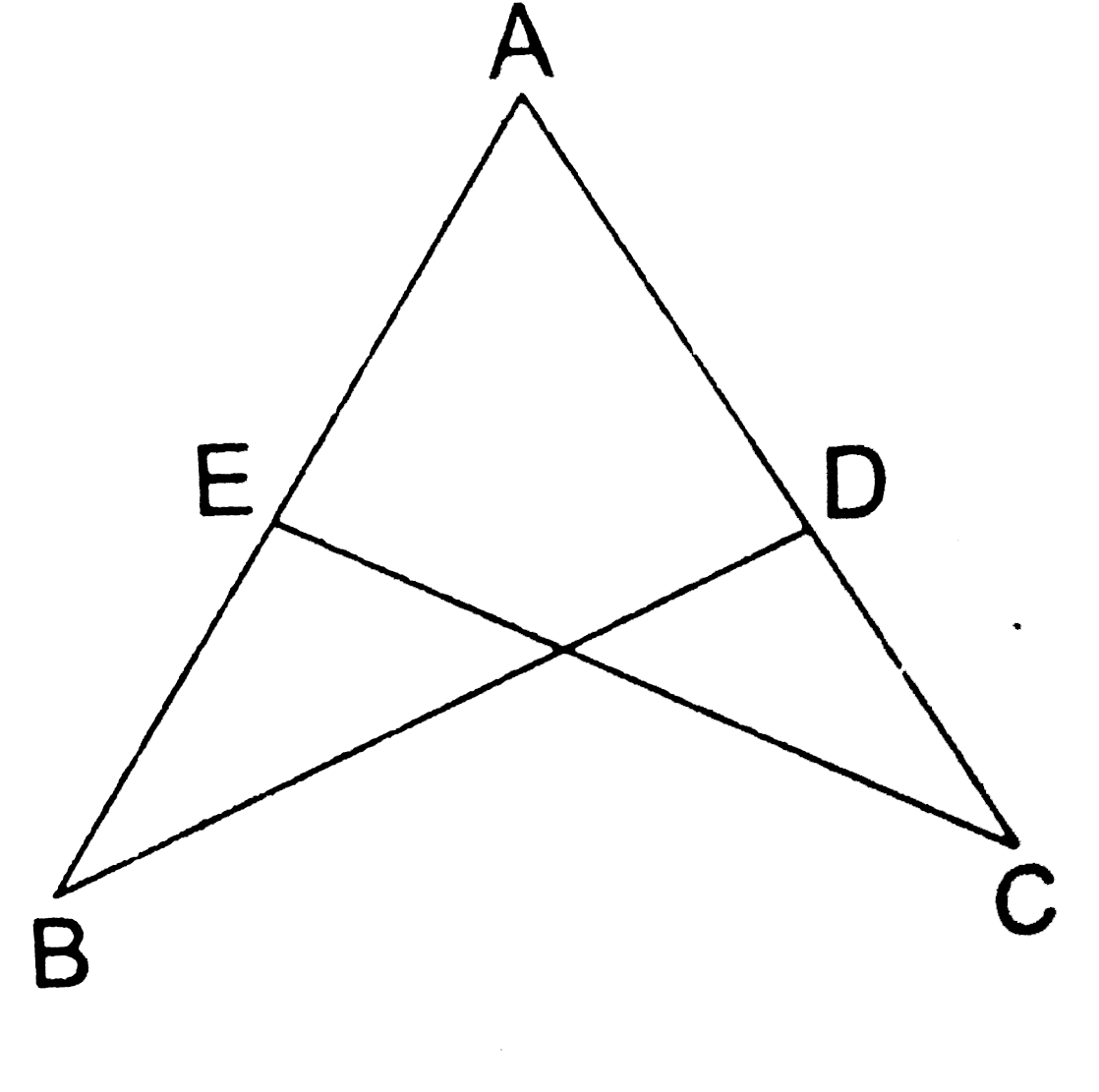
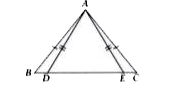
View SolutionIn the given figure, AB = AC and AD = AE. Prove that:
BD = CE
View SolutionIn the given figure, AB = CD and AD = CB. Prove that ΔABD≅ΔCDB.

View SolutionIn the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.

View SolutionIn the given figure if DE∣∣BC then find length AD
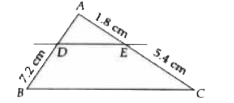
View Solution