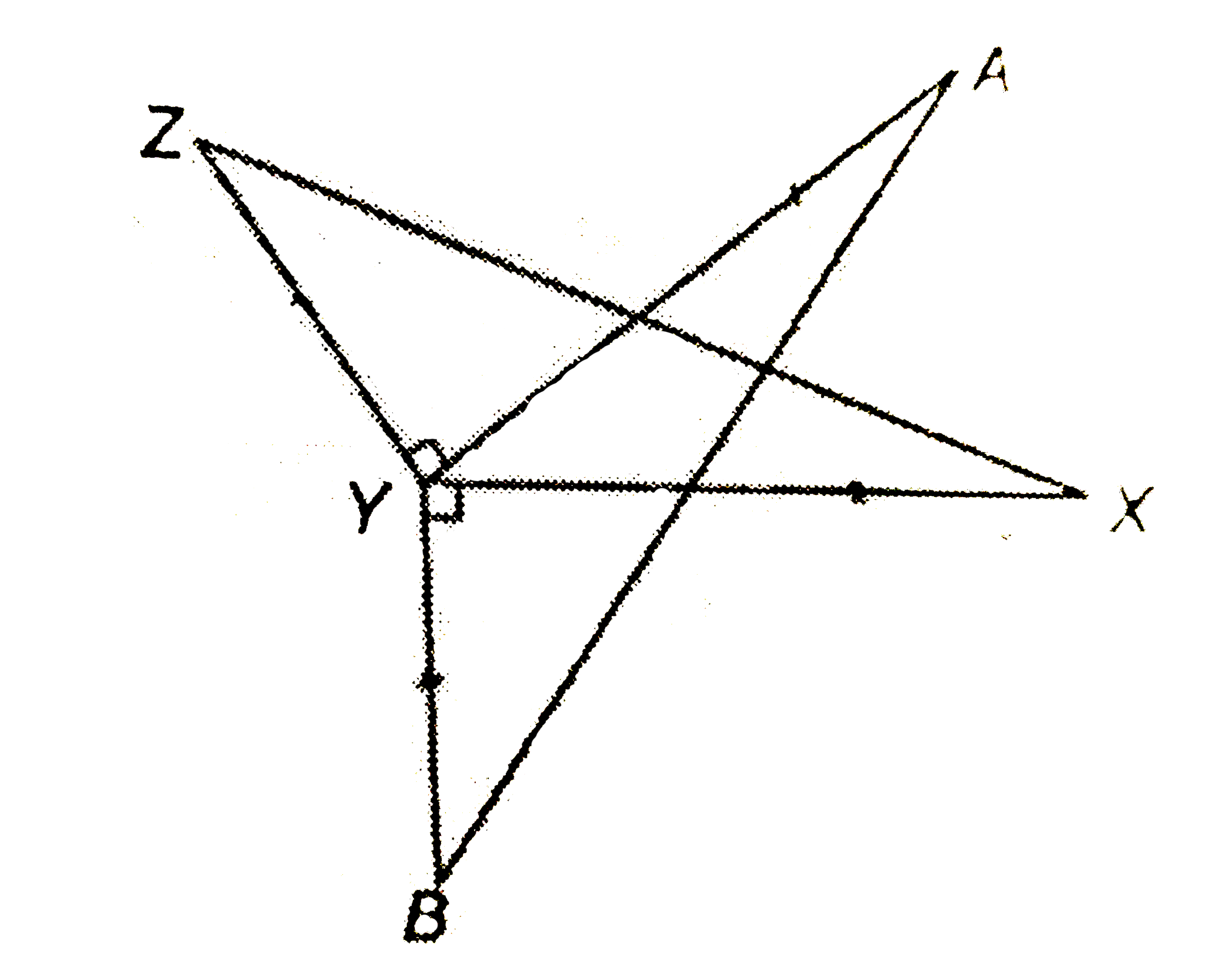
In the given figure, AY⊥ZYandBY⊥XY such that AY=ZYandBY=XY. Prove that AB=ZX.
To prove that AB=ZX given that AY⊥ZY, BY⊥XY, AY=ZY, and BY=XY, we can follow these steps:
Step 1: Understand the Given Information
We are given two right triangles, △AYB and △ZXY, where:
- AY⊥ZY implies ∠ZYA=90∘
- BY⊥XY implies ∠XYB=90∘
- AY=ZY
- BY=XY
Step 2: Analyze the Angles
From the right angles, we can state:
- ∠ZYA=90∘
- ∠XYB=90∘
Since both triangles share the angle ∠AYB and the right angles, we can express the angles in terms of the other angles:
- ∠AYB+∠ZYA=90∘
- ∠AYB+∠XYB=90∘
Step 3: Establish Angle Equality
From the above, we can conclude:
∠ZYA+∠AYB=∠XYB+∠AYB
This simplifies to:
∠ZYA=∠XYB
Thus, we have:
∠ZYX=∠AYB
Step 4: Apply the Congruence Criteria
Now we have:
1. AY=ZY (given)
2. BY=XY (given)
3. ∠AYB=∠ZYX
By the criteria of congruence (Side-Angle-Side), we can say:
△AYB≅△ZXY
Step 5: Conclude with CPCT
From the congruence of triangles, we can state:
AB=ZX
This is because corresponding parts of congruent triangles are equal (CPCT).
Final Statement
Thus, we have proved that AB=ZX.
---
We are given two right triangles, △AYB and △ZXY, where:
- AY⊥ZY implies ∠ZYA=90∘
- BY⊥XY implies ∠XYB=90∘
- AY=ZY
- BY=XY
From the right angles, we can state:
- ∠ZYA=90∘
- ∠XYB=90∘
- ∠AYB+∠ZYA=90∘
- ∠AYB+∠XYB=90∘
From the above, we can conclude:
∠ZYA+∠AYB=∠XYB+∠AYB
This simplifies to:
∠ZYA=∠XYB
Thus, we have:
∠ZYX=∠AYB
Now we have:
1. AY=ZY (given)
2. BY=XY (given)
3. ∠AYB=∠ZYX
△AYB≅△ZXY
From the congruence of triangles, we can state:
AB=ZX
This is because corresponding parts of congruent triangles are equal (CPCT).
Thus, we have proved that AB=ZX.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
In the adjoining figure, ∠AYZ=∠BYX=90∘,AY=YZ and XY=BY. Prove that AB=ZX.
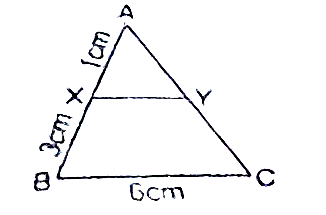
View SolutionIn the given figure , if XY||BC, find the length of XY.
View SolutionIn the given figure, BC||XY,BX||CAandAB∣∣YC. Prove that area (ΔABX)= area (ΔACY)

View SolutionIn the given figure, XY∣∣ACandXY divides ΔABC into two regions, equal in area. Find the value of AXAB
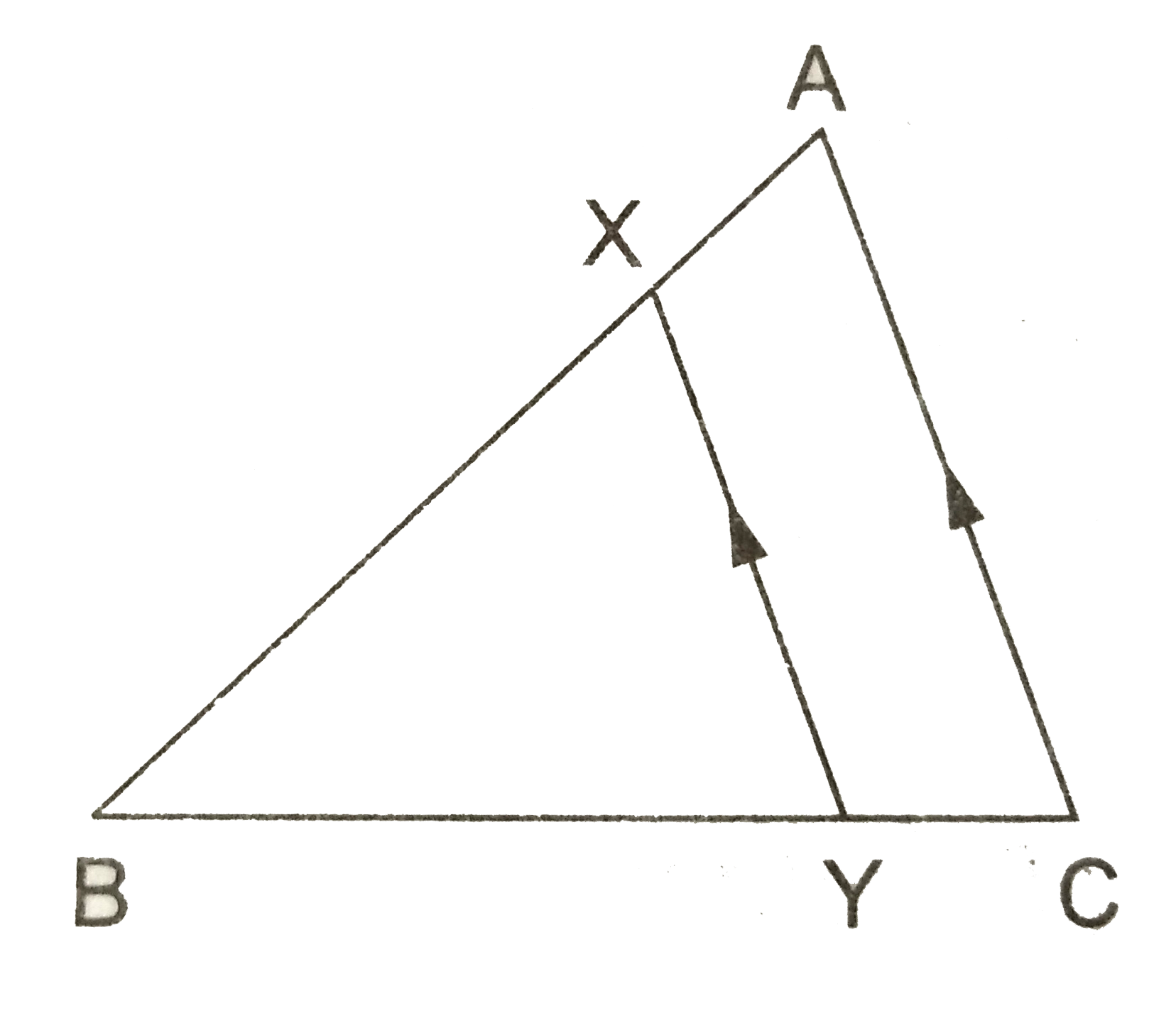
View SolutionIn given figure AX = AY, AB = AC
Show that : BX = CY
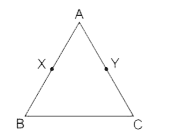
View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX = AY. Prove that CX = BY.
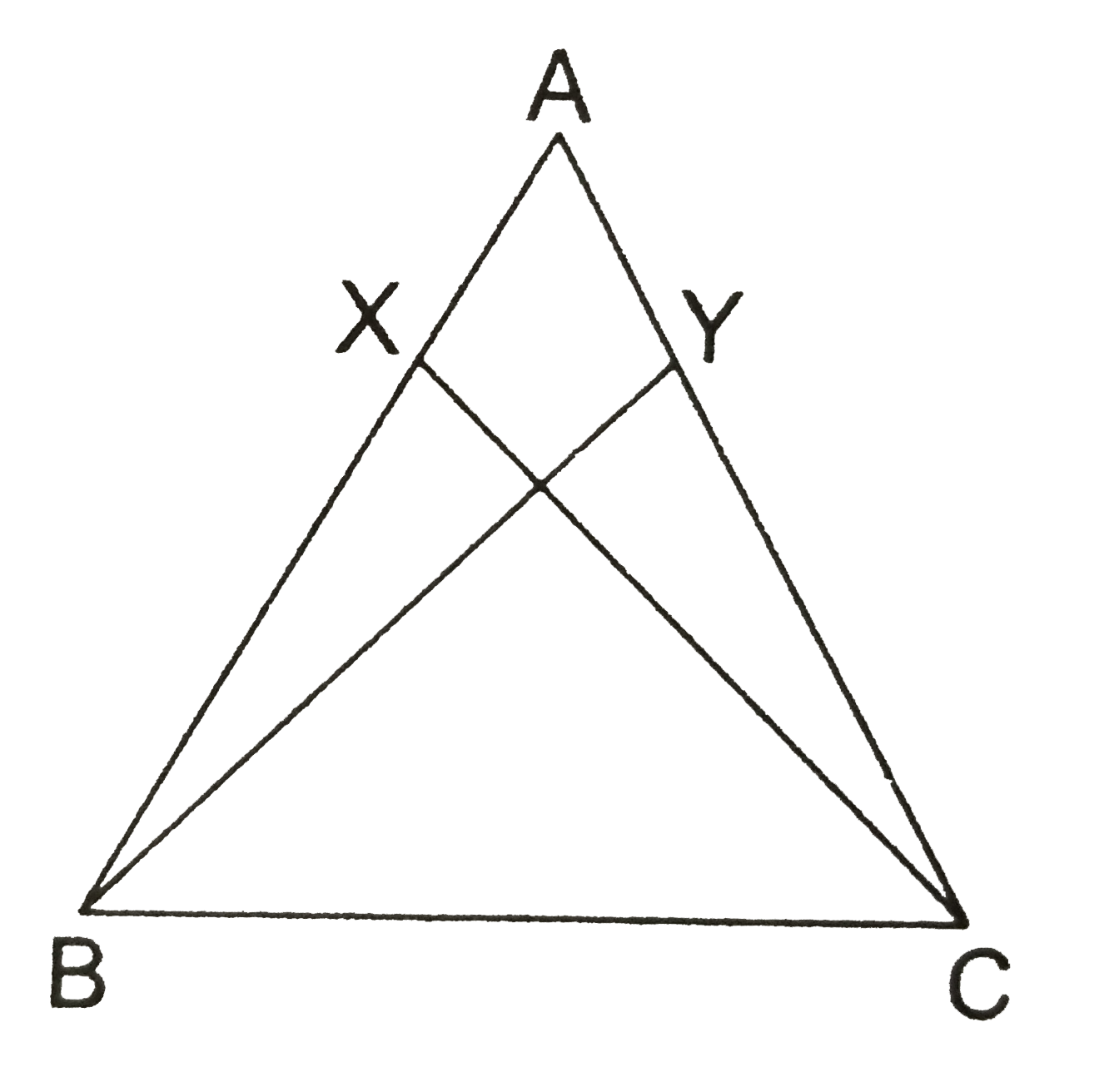
View SolutionIn Figure, X, Y are two points on equal sides AB and AC of a ABC such that AX=AY. Prove that XC=YB
View SolutionIn the given figure, line l || side BC, AP = 4, PB = 8, AY = 5 and YC= x. Find x.

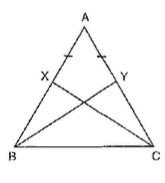
View SolutionIn Figure, X and Y are two points on equal sides AB and AC of a ABC such that AX=AY. Prove that XC=YB.
View SolutionIn the figure, line XY∣∣ side BC. AX=2, XB=4, AY=3 and YC=a then the value of a is ……. .
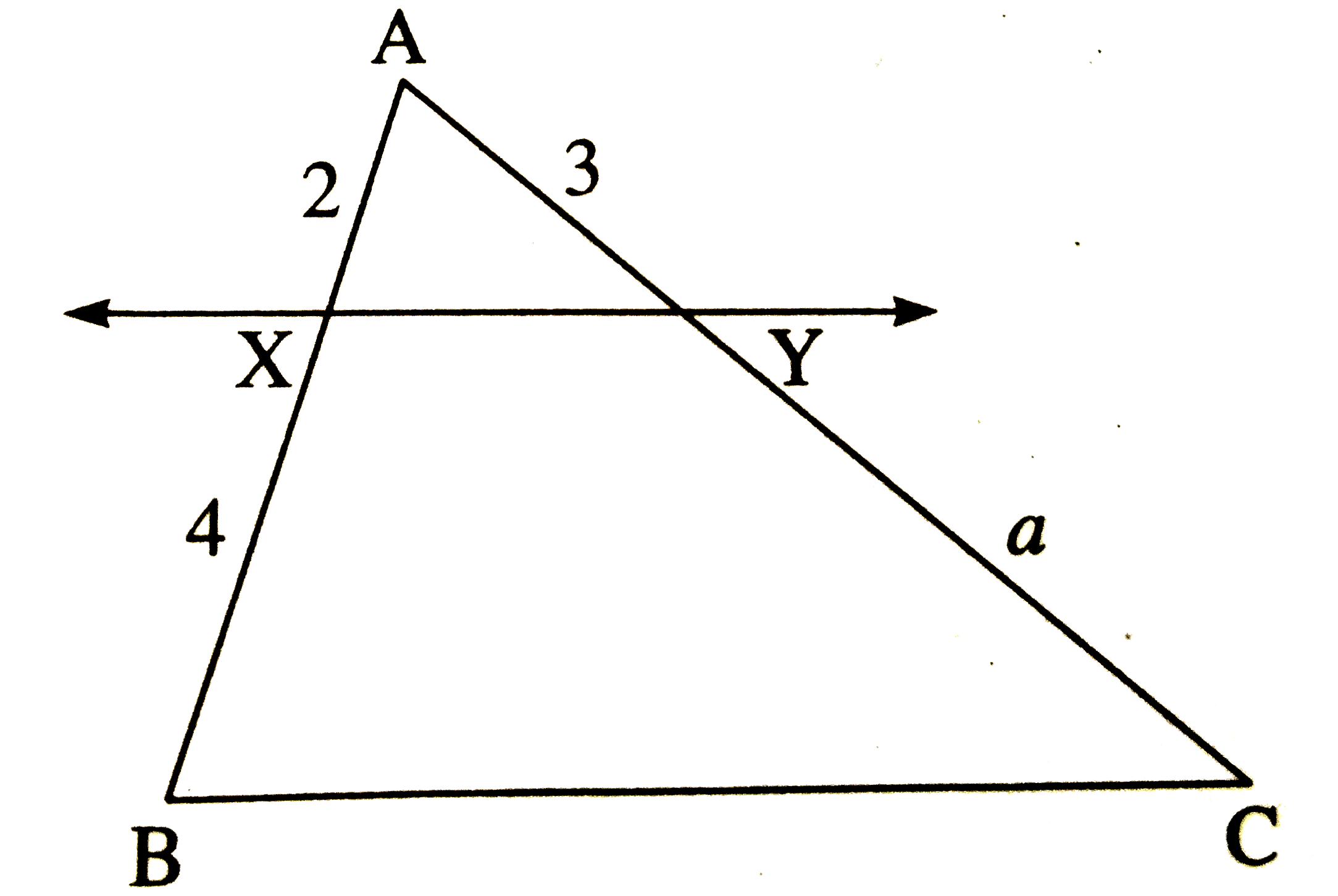
View Solution
