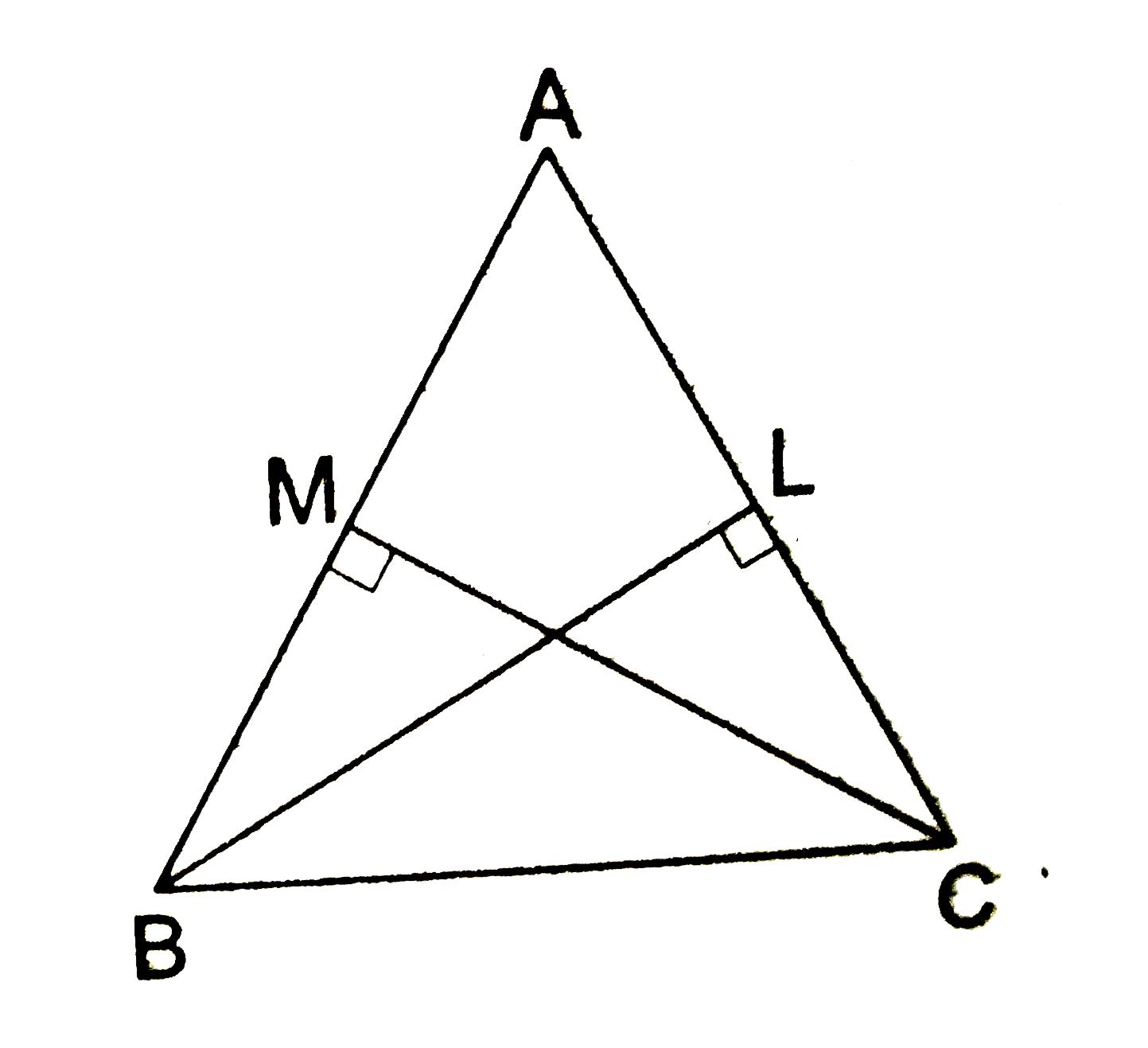
Prove that the perpendiculars drawn from the vertices of equal angles of an isosceles triangle to the opposite sides are equal.
Given AΔABC in which ∠BCA=∠CBA,B⊥ACandCM⊥AB,
TO PROVE BL = Cm.
PROOF In ΔBCLandΔCBM, we have
∠BCL=∠CBM [∵∠BCA=∠CBA],
∠BLC=∠CMB=90∘
and BC = CB (common)
∴ΔBCL≅ΔCBM (AAS-criteria).
Hence, BL = CM (c.p.c.t.).
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
The perpendiculars drawn from the vertices to the opposite sides of a triangle, meet at the point whose name is
AincentreBcircumcentre barCcentroidDorthocentre
Altitudes the perpendiculars drawn from the vertices of a triangle to the opposite side are known as the altitudes of the triangle.
View SolutionShow that in an isosceles triangle, the angles opposite to the equal sides are equal.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
View SolutionProve that the bisector of the vertical angle of an isosceles triangle bisects the base at right angles.
View SolutionIf ΔABC is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionIf ABC is an isosceles triangle with AB=AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View Solution
