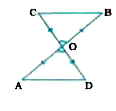
In the given figure, Oa = OB and OC = OD. Which is the criteria to prove
ΔAOC≅ΔBOD.

A
SAS
B
ASA
C
SSS
D
NONE OF THESE
Video Solution
Text Solution
The correct Answer is:A
(i) In ΔOACandΔOBD, we have
Oa = OB (given),
OC = OD (given)
and ∠AOC=∠BOD (vertically opposite ∠s).
∴ ΔOAC≅ΔOBD (by SAS-criteria).
(ii) We have, ΔOAC≅ΔOBD (proved above)
∴ ∠OAC=∠OBD (c.p.c.t).
But, there are alternate angles.
∴ AC||BD.
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9A
Explore 27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9B
Explore 16 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 22 Videos
Similar Questions
Knowledge Check
In the given figure, OA = OB, OC = OD, ∠AOB=∠COD. Which of the following statements is true?
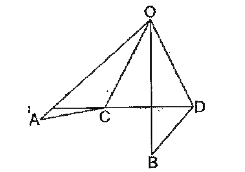 AAC = CDBOA=ODCAC=BDD∠OCA=∠ODC
AAC = CDBOA=ODCAC=BDD∠OCA=∠ODCIn the given figure, rays OA, OB, OC and OD are such that ∠AOB = 50∘ , ∠BOC = 90∘, ∠COD=70∘ and ∠AOD=x∘. Then, the value of x is
 A50∘B70∘C150∘D90∘
A50∘B70∘C150∘D90∘
In the givne figure, OA = OB and OP = OQ.
Prove that (i) PX = QX, (ii) AX = BX.
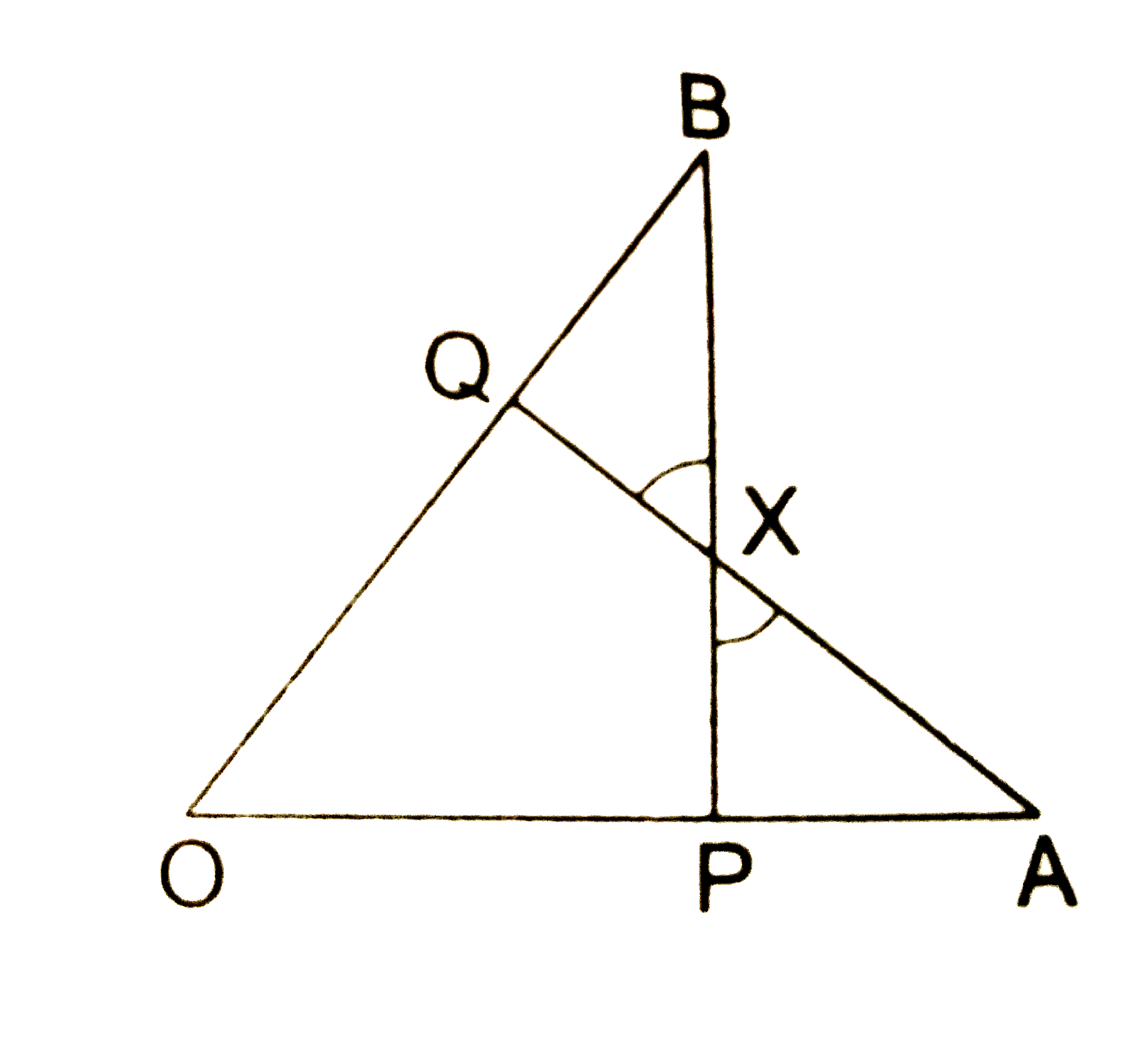
View SolutionIn the given figure, OA=OB and OP=OQ. Prove that (i) PX=QX, (ii) AX=BX
View SolutionIn the given figure, ray OC is the bisector of ∠AOB and OD is the ray opposite to OC. Show that ∠AOD=∠BOD.

View SolutionIn the given figure, OC.OD = OA.OB
Show that : ∠A=∠D and ∠C=∠B.

View SolutionIn the figure given below, OD=OC=OB. Find ∠DCB.
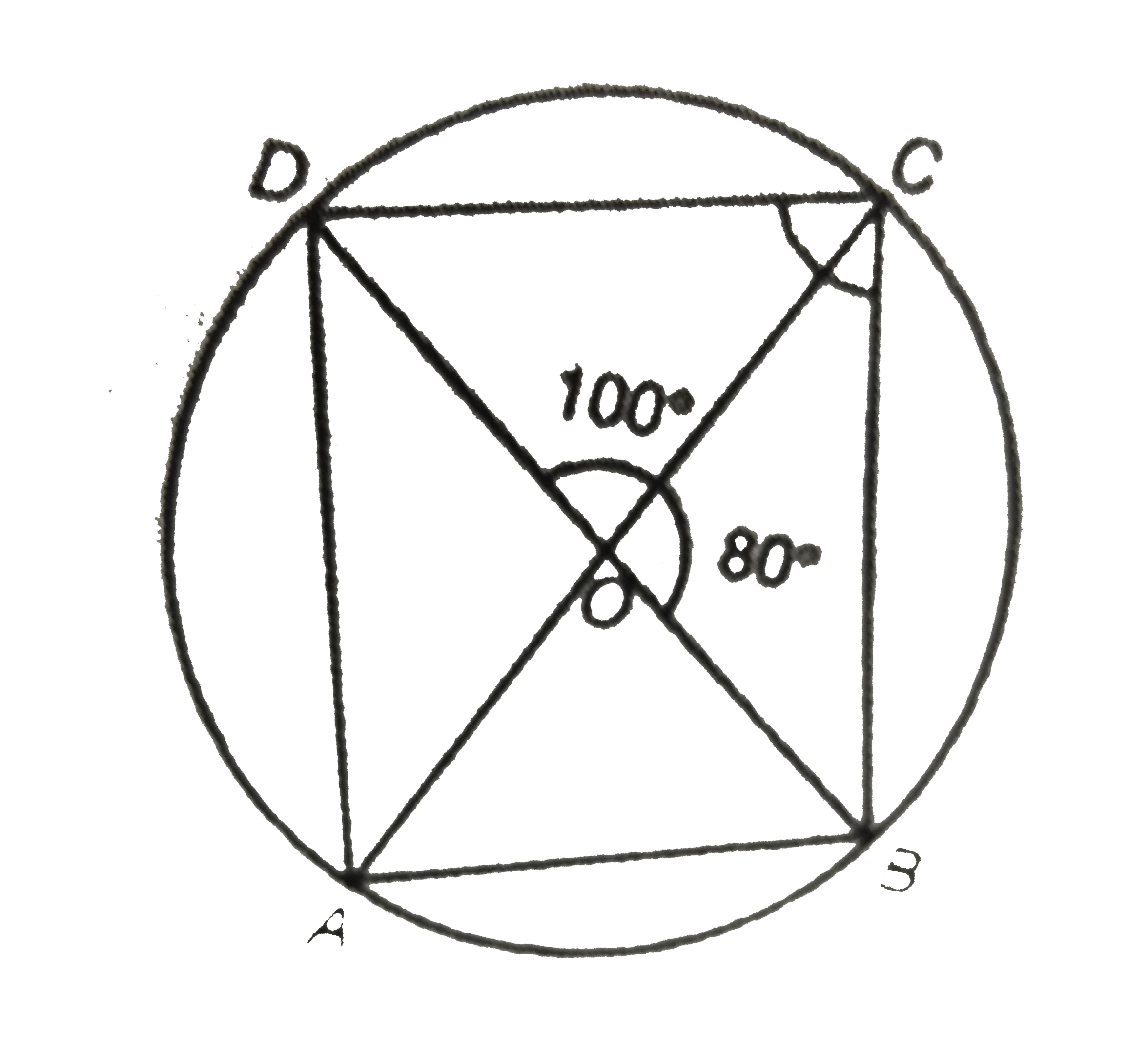
View SolutionIn the given figure,rays OA,OB,OC and OD are such that ∠AOB=56∘,∠BOC=100∘,∠COD=x∘ and ∠DOA=74∘,Find the value of x.
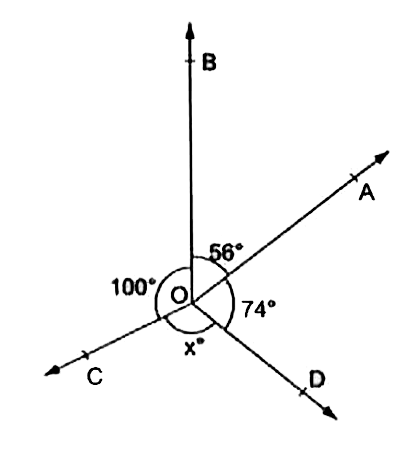
View Solution