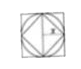
The side of a square is 10 cm. Find the area of circumscribed and in

The length of the side of a square is 14 cm. Find out the ratio of the radii of the inscribed and circumscribed circle of the square.
AA) $\sqrt{2} : 1$
BB) $1 : \sqrt{2}$
CC) $\sqrt{2} : 3$
DD) $2 : 1$
If the side of a square is 24 cm, then the circumference of its circumscribed circle ( in cm ) is :
A $24 \sqrt{3} π$
B $24 \sqrt{2} π$
C $12 \sqrt{2} π$
D $24 π$
If the side of a square is 24 cm, then the circumference of its circumscribed circle ( in cm ) is :
A $24 \sqrt{3} π$
B $24 \sqrt{2} π$
C $12 \sqrt{2} π$
D $24 π$

The side of a square is 10 cm. Find the area of circumscribed and inscribed circles.