An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression where r is the radius of the circle.
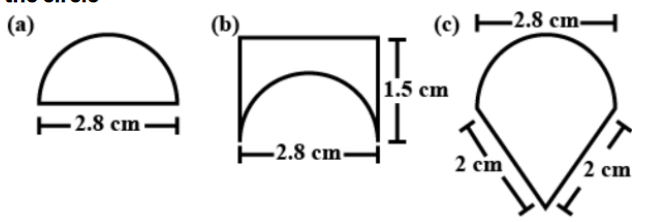
(a) Radius of the semicircle part=
Perimeter of the circle= r
Perimeter of the semicircle =
The perimeter of the food piece=
(b). Radius of semicircle part=
Perimeter of the food piece
(c). Radius of the food piece=
Perimeter of the food piece
Thus, the ant will have to take a longer round for food
piece (b) because the
perimeter of
the figure given in (b) is the
greatest among all
Topper's Solved these Questions
- MENSURATIONBOOK - NCERTCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.4
8 Videos
- MENSURATIONBOOK - NCERTCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.3
10 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERTCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - EXERCISE 2.3
9 Videos
- PLAYING WITH NUMBERSBOOK - NCERTCHAPTER - PLAYING WITH NUMBERSEXERCISE - SOLVED EXAMPLES
8 Videos
Similar Questions
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c=2πr, where r is the radius of the circle.

View SolutionA particle is moving in a circle of radious R with constant speed. The time period of the particle is T = 1s. In a time interval T6, if the difference between average speed and the magnitude of average velocity of the particle is 2m/s, then report 49R50, where R is the radius of the circle (in metres) (take π=3.14 )
View Solution
Knowledge Check
The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.

An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Variable magnetic fluxAcan chane sinusoidallyBshould either increase or decrease all the timeCmust becomes zero when induced field is maximumDnone of theseThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
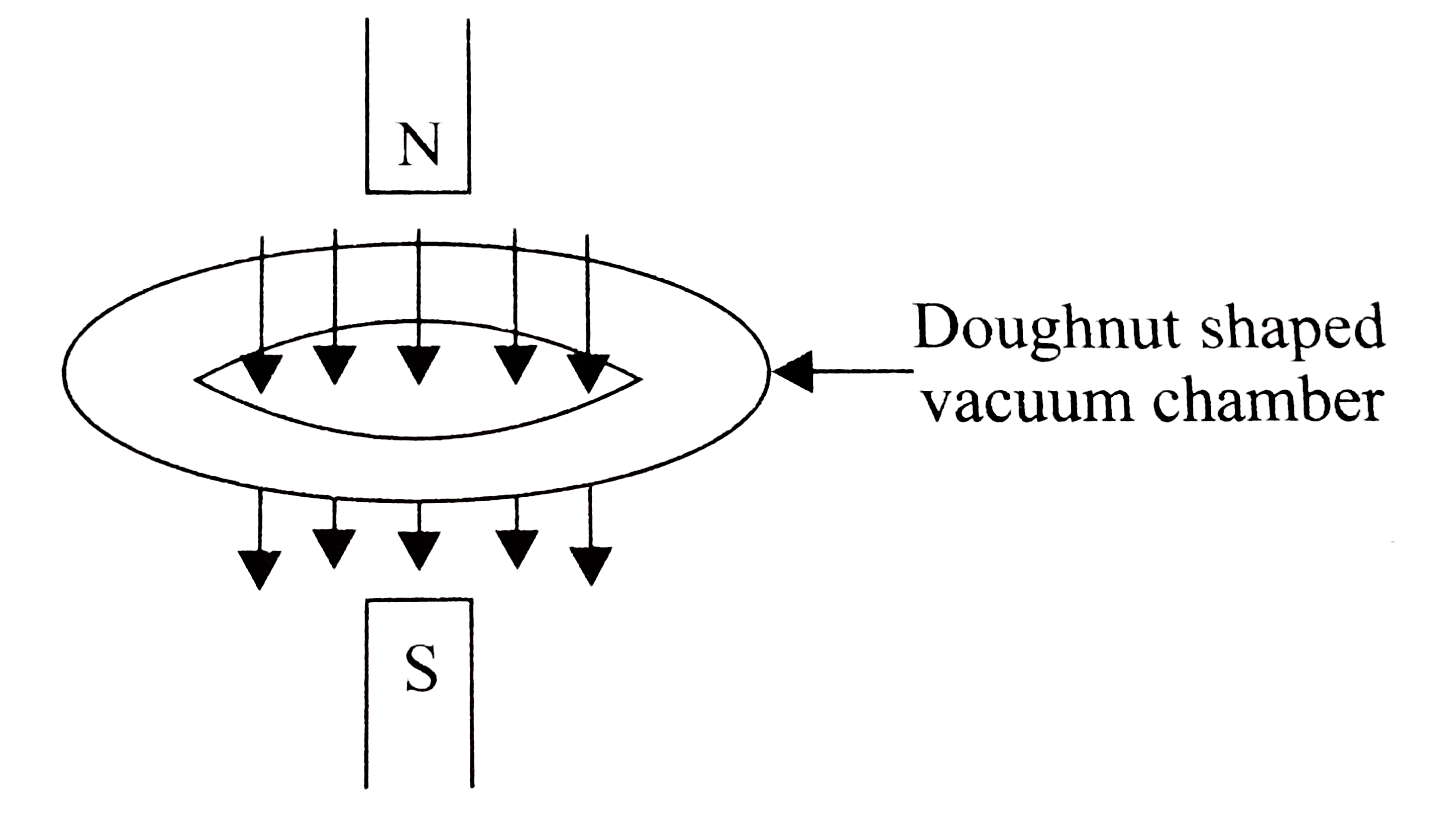
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Working of betatron is not based upon which of the following theories?Achanging magnetic flux induces electric fieldBcharged particles at rest can be accelerated only by electric fieldsCmagnetic fields can apply a force on moving charges which is perpendicular to both magnetic field and motion of the particleDβ particles are emitted in radioactive decay process.A tap drips at a rate of one drop/sec. 600 drops make 100 ml. The number of liters wasted in 400 days is :
A5760B57600C576000D5760000
Let C1,C2,,Cn be a sequence of concentric circle. The nth circle has the radius n and it has n openings. A points P starts travelling on the smallest circle C1 and leaves it at an opening along the normal at the point of opening to reach the next circle C2 . Then it moves on the second circle C2 and leaves it likewise to reach the third circle C3 and so on. Find the total number of different path in which the point can come out of nth circle.
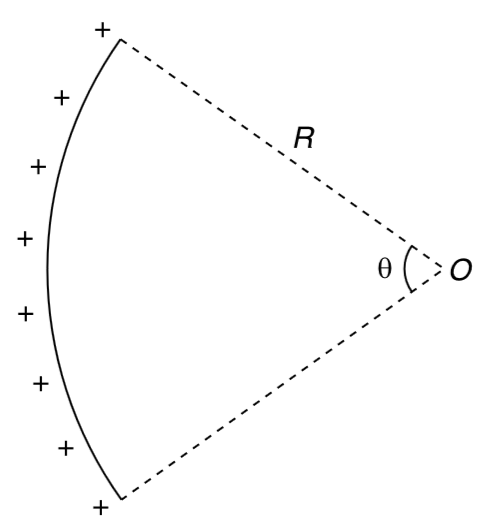
View SolutionA thread having linear charge density λ is in the shape of a circular arc of radius R subtending an angle θ at the centre.
(a). Find the electric field at the centre.
(b). Using the epression obtained in part (a) find the field at the centre if the thread were emicircular
(c). Find the field at centre using the expression obtained in part (a) for the case θ→0. Is the result justified?
(d). A thread having total charge Q (uniformly distributed is in the shape of a circular arc of radius R subtending an angle θ at centre. write the expression for the field at the center. Obtain the field whenθ→0. Make sure you understand the difference in case. (c) and (d).
View Solution(a) A uniform chain is lying in form of on arc of a circle of radius R. The arc subtends an angle of 2α at the centre of the circle. Find the distance of the centre of mass of the chain from the centre of the circle.
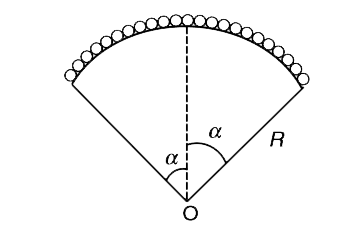
(b) A uniform chain of length πR2 is lying symmetrically on the top of a fixed smooth half cylinder (see figure) of radius R. The chain is pulled slightly from one side and released. It begins to slide. Find the speed of the chain when its one end just touches the floor. What is speed of centre of mass of the chain at this instant ?
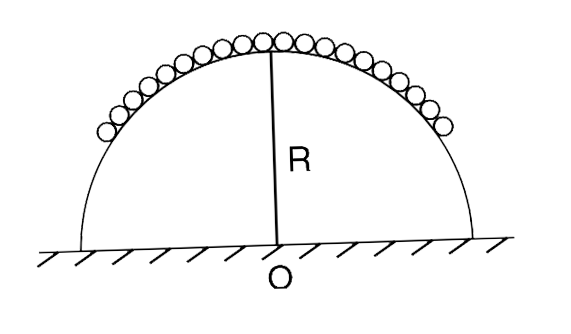
(c) In part (b) assume that the half cylinder is not fixed and can slide on the smooth floor. Find the displacement of the cylinder by the time one end of the chain touches the floor. Mass of cylinder is equal to that of the chain. For part (b) and (c) assume that the chain remains in contact with the cylinder all the while.
View SolutionUsing Rautherfold model of the atom, derive the expression for the total electron in hydrogen atom. What is the significance of total negative energy possedssed by the electron?
Using Bohr's postulates of the atomic model, derive the expression for radius of nth electron orbit. Hence obtain the expression for Bohr's radius
This therory developed is applicable to Hydrogen atoms and ions having just one electron. Let us assume that the nucleus has a positive charge Ze (i.e. ther are Z protons in it) and electrons moves with a consant speed V along a circle of radius r with the centre at nucleus By Coulomb's law
View SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
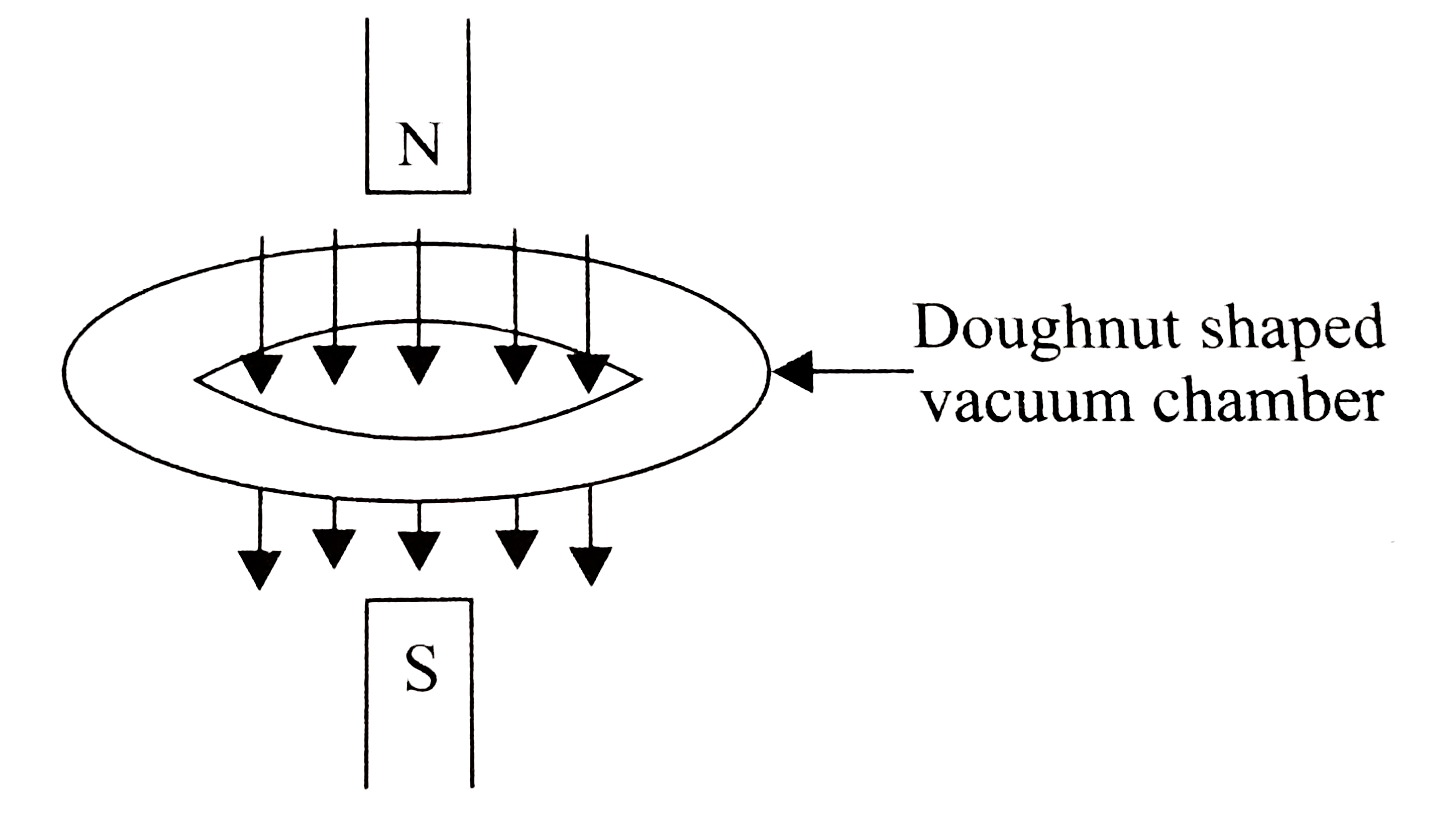
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Magnetic field which keeps the particles in circular path must
View Solution
