A particle is moving in a circle of radious R with constant speed. The time period of the particle is T = 1s. In a time interval T6, if the difference between average speed and the magnitude of average velocity of the particle is 2m/s, then report 49R50, where R is the radius of the circle (in metres) (take π=3.14 )
The correct Answer is:7
2πω1s
ω=2π rad/s
Δθ=ωΔt=2π×16=π3 rad

avg-speed =2Rπ
avg. velocity =displacementtime=ΔxΔt
→xi=Rˆj
→xf=Rcos(π3)ˆj+Rsin(π3)ˆi
=R[12ˆj+√32ˆi]
Δ→x=−R2ˆj+√32Rˆi
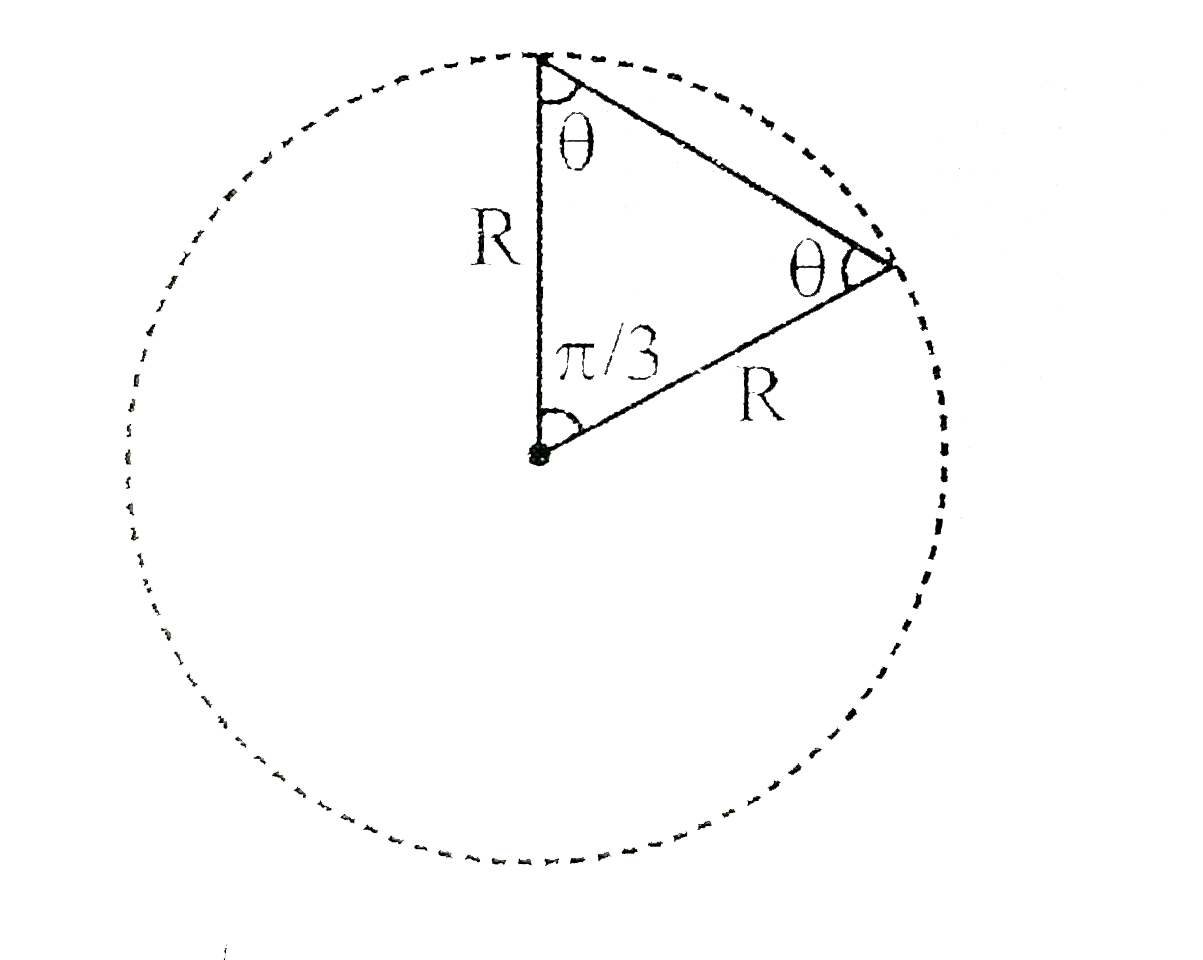
|Δ→x|=R√14+34=R
or 2θ+π3=π
θ=π3
equilateral triangle
So |Δ→x|=R
|avg.velocity|=R1/6=6R
6.28R−6R=0.28R=2
R=228×100=507
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART A
Explore 35 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART B
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A particle is moving in a circle of radius R with constant speed. The time period of the particle is t=1. In a time t=T/6, if the difference between average speed and average velocity of the particle is 2ms−1. Find the radius R of the circle (in meters).
View SolutionA particle is moving in a circle of radius R with constant speed. The time period of particle is T=1s. In a time t=T6, the difference between the average speed and the average velocity of the particle is 2ms. Find the radius R (in metres) of the circle. (Take π=227)
View Solution
Knowledge Check
A particle is moving in a circle of radius R with constant speed. The time period of the particle is T. In a time t=T6
Average speed of the particle is ……AπR6TB2πR3TC2πRTDRTA particle is moving in a circle of radius R with constant speed. The time period of the particle is T. In a time t=T6
Average velocity of the particle is…..A3RTB6RTC2RTD4RTIf a particle covers half the circle of radius R with constant speed then
AMomentum change is mvrBChange in K.E is 1/2mvCChange in K.E is mvDChange in K.E is zero
A particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2π. The acceleration of the particle is:
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionA particle moves in circle of radius R with a constant speed v. Then, find the magnitude of average
acceleration during a time interval πR2v.
View SolutionIf a particle is moving along a circle of radius 3 m with a constant speed 9m/s, then it covers a quarter of the circle in time of
View Solution

