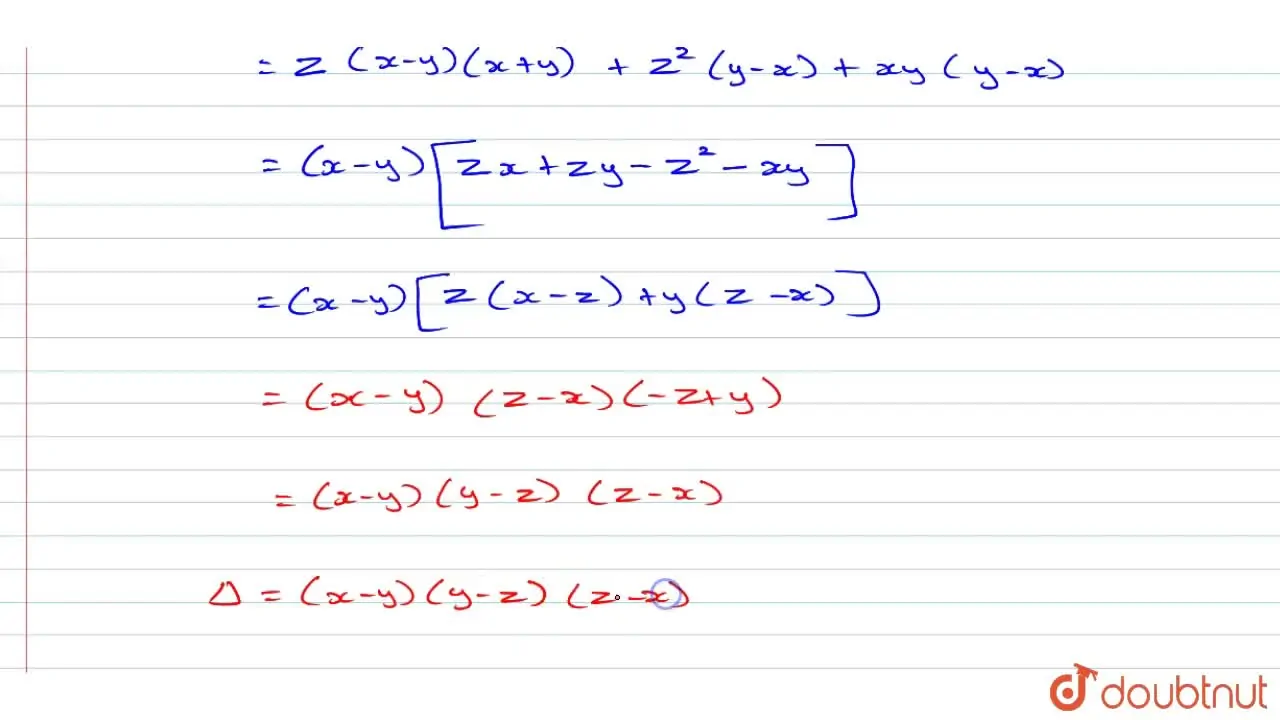Using Cofactors of elements of third column , evaluate , Solution in Tamil
The correct Answer is:
Step by step video, text & image solution for Using Cofactors of elements of third column , evaluate , Delta ={:[( 1,x,yz),(1,y,zx),( 1,z,xy) ]:} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - NCERT TAMILCHAPTER - DETERMINANTS EXERCISE - EXERCISE 4.517videos
DETERMINANTS
- BOOK - NCERT TAMILCHAPTER - DETERMINANTS EXERCISE - EXERCISE 4.616videos
DETERMINANTS
- BOOK - NCERT TAMILCHAPTER - DETERMINANTS EXERCISE - EXERCISE 4.37videos
DETERMINANTS
- BOOK - NCERT TAMILCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - MISCELLANEOUS EXERCISE ON CHAPTER 523videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERT TAMILCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - MISCELLANEOUS EXERCISE18videos
DIFFERENTIAL EQUATIONS
Similar Questions
Find adjoint of each of the matrices
[1234]04:24View SolutionExamine the consistency of the system of equations
x+2y=2
2x+3y=304:24View SolutionFind area of the triangle with vertices at the point given in each of the following:
(1,0),(6,0),(4,3)08:15View SolutionDifferentiate w.r.t.x the function in Exercises 1 to 11.
(3x2−9x+5)908:15View SolutionFor each of the differential equations given below, indicate its order and degree(if defined).
(i) d2ydx2+5x(dydx)2−6y=logx
(ii)(dydx)3−4(dydx)2+7y=sinx
(iii)d4ydx4−sin(d3ydx3=006:45View SolutionUsing Cofactors of elements of third column, evaluate Δ=∣∣ ∣ ∣∣1xyz1yzx1zxy∣∣ ∣ ∣∣
06:13View Solutionतीसरे स्तंभ के अवयवों के सहखंडो का प्रयोग करके Δ=∣∣ ∣ ∣∣1xyz1yzx1zxy∣∣ ∣ ∣∣ का मान ज्ञात कीजिये ।
07:11View Solutionतीसरे स्तम्भ के अवयवों के सहखंडो का प्रयोग करके Δ=∣∣ ∣ ∣∣1xyx1yzx1zxy∣∣ ∣ ∣∣ का मान ज्ञात कीजिए।
08:29View Solutionतीसरे स्तम्भ के अवयवों के सह-खण्डों का प्रयोग करके Δ=∣∣ ∣ ∣∣1xyz1yzx1zxy∣∣ ∣ ∣∣ का मान ज्ञात कीजिए ।
04:55View Solutionतीसरे स्तम्भ के अवयवों के सहखंडो का प्रयोग करके Δ=∣∣ ∣ ∣∣1xyz1yzx1zxy∣∣ ∣ ∣∣ का मान ज्ञात कीजिए :
04:06View SolutionUsing Cofactors of elements of third column , evaluate , Δ=⎡⎢⎣1xyz1yzx1zxy⎤⎥⎦
04:52View SolutionUsing Cofactors of elements of third column , evaluate , Δ=∣(1,x,yz),(1,y,zx),(1,z,xy)|}
02:54View SolutionUsing Cofactors of elements of third column , evaluate , Δ=∣(1,x,yz),(1,y,zx),(1,z,xy)|}
04:13View SolutionUsing Cofactors of elements of third column, evaluate Δ=∣∣ ∣ ∣∣1xyz1yzx1zxy∣∣ ∣ ∣∣
06:56View SolutionUsing Cofactors of elements of third column , evaluate Δ=∣∣ ∣ ∣∣1xyz1yzx1zxy∣∣ ∣ ∣∣
05:28View Solution