If the chord joining points P(α)andQ(β) on the ellipse (x2a2)+(y2b2)=1 subtends a right angle at the vertex A(a,0), then prove that tan(a2)tan(β2)=−b2a2.
mPA×mQA=−1
orbsinαacosα−a×bsinβacosβ−a=1
or4sin.α2cos.α2sin.β2cos.β2(2sin2.α2)(2sin2.β2)=−a2b2
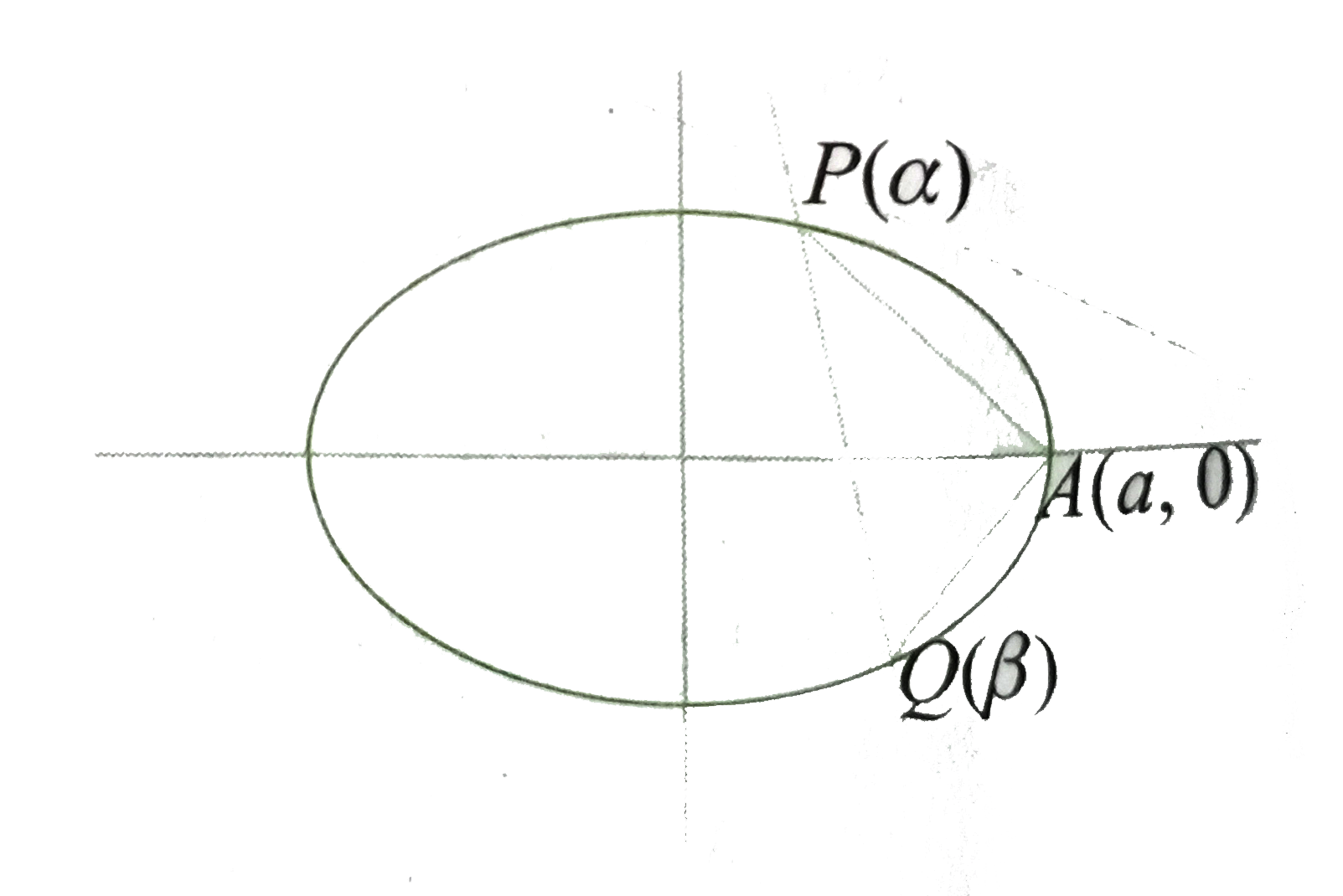
or tan.α2tan.β2=−b2a2
Similar Questions
If the chord joining points P(α)andQ(β) on the ellipse (x2a2)+(y2b2)=1 subtends a right angle at the vertex A(a,0), then prove that tan(a2)tan(β2)=−b2a2.
View SolutionIf tanθ1.tanθ2=a2b2 then the chord Joining two points θ1andθ2 on the ellipse x2a2+y2b2=1 will subtend a right angle at (A) focus (B) centre (C) end of the major axis (D) end of the major axis
View Solution
Knowledge Check
If a chord PθQϕ of an ellipse x2a2+y2b2=1 subtands a right angle at the vertex A (a,0), then
tan(θ2)⋅tan(ϕ2)=A−a2b2B−b2a2C−b2aD−abIf a chord PQ , joining P (θ) Q and (ϕ) , of an ellipse
x2a2+y2b2=1 , subtands a right angle at its centre , then
tanθ⋅tanϕ =Aa2b2B−b2a2C−a2b2Db2a2P is any point lying on the ellipse x2a2+y2b2=1(a>b) whose foci are S and S'. If ∠PSS'=aand∠PS'S=β, then the value of tan.α2tan.β2 is
A1+e1−eB1+e21−e2C1−e1+eD1
If the chord, joining two points whose eccentric angles are αandβ, cuts the major axis ofthe ellipse x2a2+y2b2=1 at a distance c fromn the centre, then tanα/2.tanβ/2 is equal to
View Solutionif 2tanβ+cotβ=tanα then prove that cotβ=2tan(α−β)
View SolutionThe condition that the chord of the ellipse x2/a2+y2/b2=1, whose middle point is (x1,y1) subtends a right angle at the centre of the ellipse is .......... .
View SolutionIf a chord joining two points whose eccentric angles are αandβ so that tanα.tanβ=−a2b2 , subtend an angle θ at the centre of the ellipse x2a2+y2b2=1 then θ=
View Solutionif c⊗x=cosα.cosβ then prove that tan(x+α2)⋅tan(x−α2)=tan2β2
View Solution
