Question

P is any point lying on the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b)$ whose foci are $S$ and $S\text{'}$. If $\angle PSS\text{'}=a\text{and}\angle PS\text{'}S=\beta$, then the value of $\tan .\frac{\alpha }{2}\tan .\frac{\beta }{2}$ is

Options

A. `(1+e)/(1-e)`
B. `(1+e^(2))/(1-e^(2))`
C. `(1-e)/(1+e)`
D. 1

Answer

C

Explanation

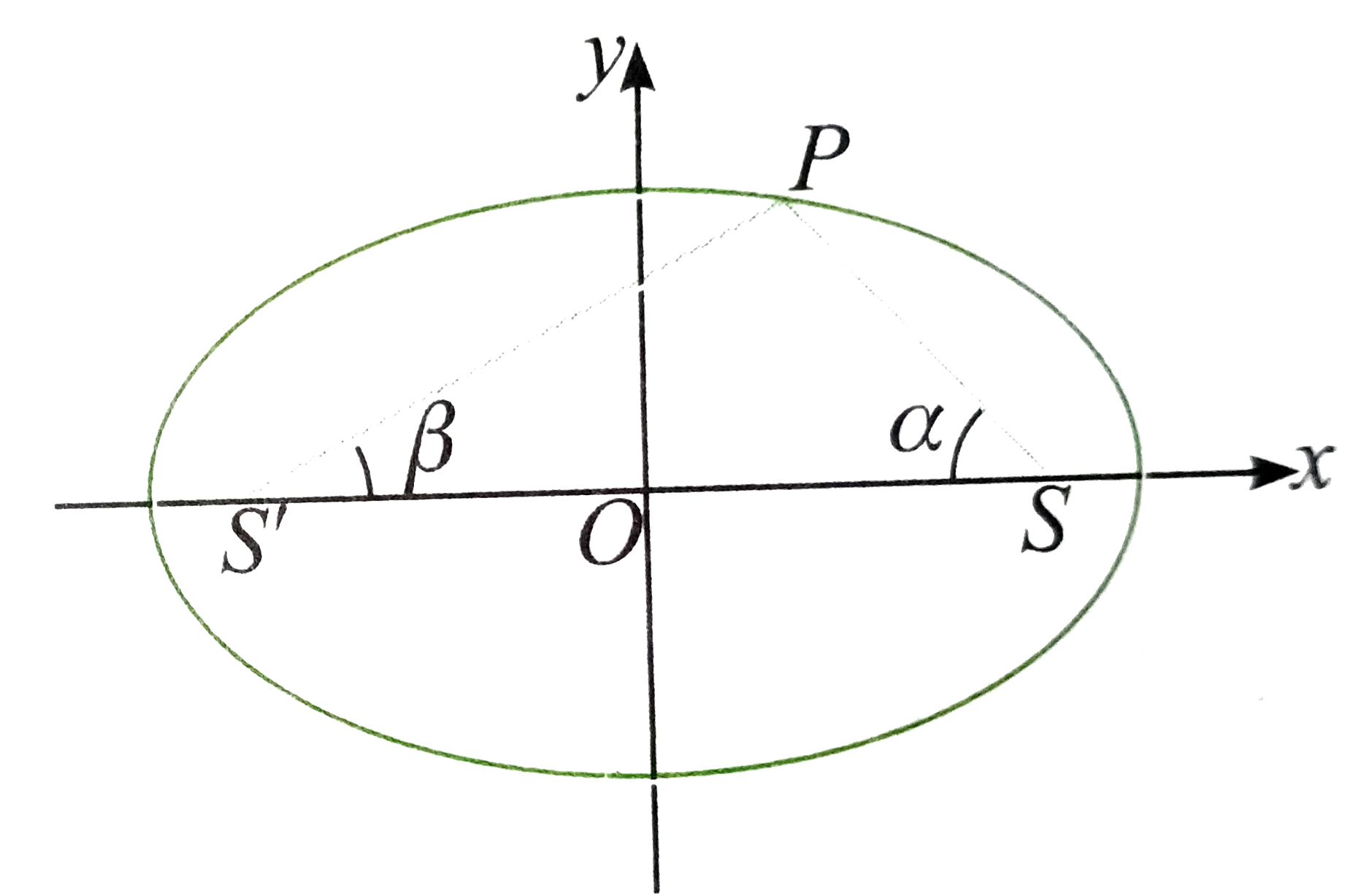
SP+S''P=2a
In `DeltaSPS''`
Perimeter, `2s=SP+S'P+SS'=2a+2ae=2a(1+e)`
Now, `tan.(alpha)/(2)tan.(beta)/(2)=sqrt(((s-b)(s-c))/(s(s-c)))sqrt(((s-a)(s-c))/(s(s-b)))`
`s(-c)/(s)=(2s-2c)/(2s)=(2a(1+e)-2c)/(2a(1+e))`
`(2a+2ae-4ae)/(2a(1+e))=(2a(1-e))/(2ae(1+e))`
`:.tan.(alpha)/(2)tan.(beta)/(2)=(1-e)/(1+e)`