If P is any point on ellipse with foci S1&S2 and eccentricity is 12 such that ∠PS1S2=α,∠PS2S1=β,∠S1PS2=γ , then cot(α2),cot(γ2),cot(β2) are in
Video Solution
Text Solution
We know that
tan.α2tan.β2=1−e1+e=1−(1/2)1+(1/2)=13
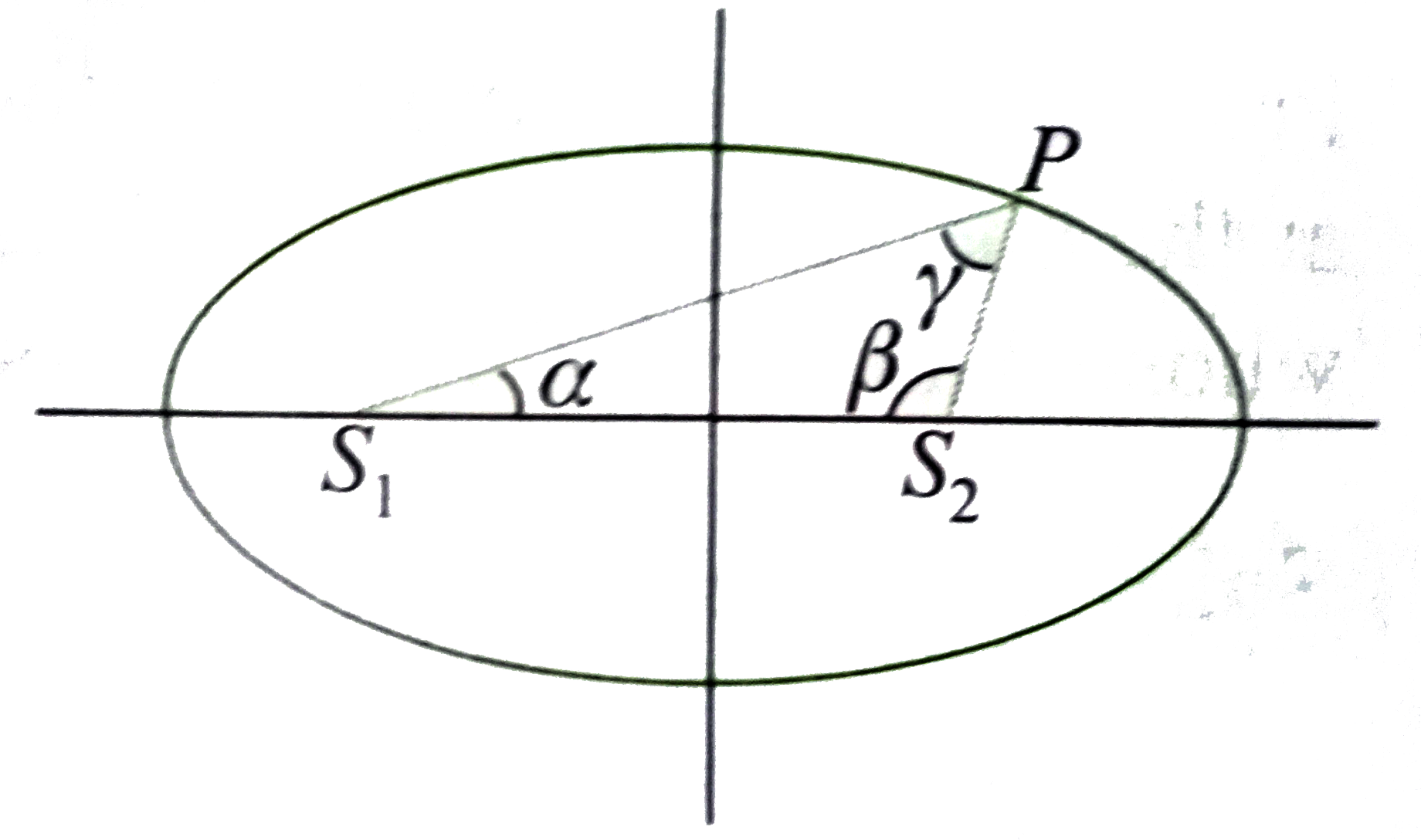
In triangle ABC, we know that
tan.A2tan.B2+tan.C2tan.B2+tan.C2tan.A2=1
or cot.A2+cot.B2+cot.C2=cot.A2cot.B2cot.C2=1
For ΔPS1S2
cot.α2+cot.β2+cot.γ2=3cot.γ2
or 2cot.γ2=cot.α2+cot.β2
Therefore, cot,α/2,cotγ/2,cotβ/2 are in AP
|
Similar Questions
Knowledge Check
If P is a point on the ellipse x216+y225=1 whose foci are S and S', then PS+PS'=8.
A6B8C10D12If P is any point on the ellipse x236+y216=1 and S and S', are the foci, then PS+PS'equal to
A4B8C10D12If P is a point on the ellipse X29+y24=1
whose foci are S and S' then the value of PS + PS' isA6B4C3D2
If P is a point on the ellipse x216+y/(20)=1, whose foci are S and S'. Then PS+PS' is equal to
View SolutionP is a variable point on the ellipse with foci S1 and S2. If A is the area of the the triangle PS1S2, the maximum value of A is
View SolutionIf P is a point on the ellipse x216+y225=1 whose foci are S and S', then PS+PS'=8.
View SolutionP is any point lying on the ellipse x2a2+y2b2=1(a>b) whose foci are S and S'. If ∠PSS'=aand∠PS'S=β, then the value of tan.α2tan.β2 is
View SolutionIf tanβ=2sinαsinγcosec(α+γ), then cotα,cotβ,cotγ are in
View Solution