A line passing through the origin intersects two concentric circles of radii at If the lines parallel to the X-and Y-axes through respectively, meet at point then find the locus of
Let
From the fiugure,
and
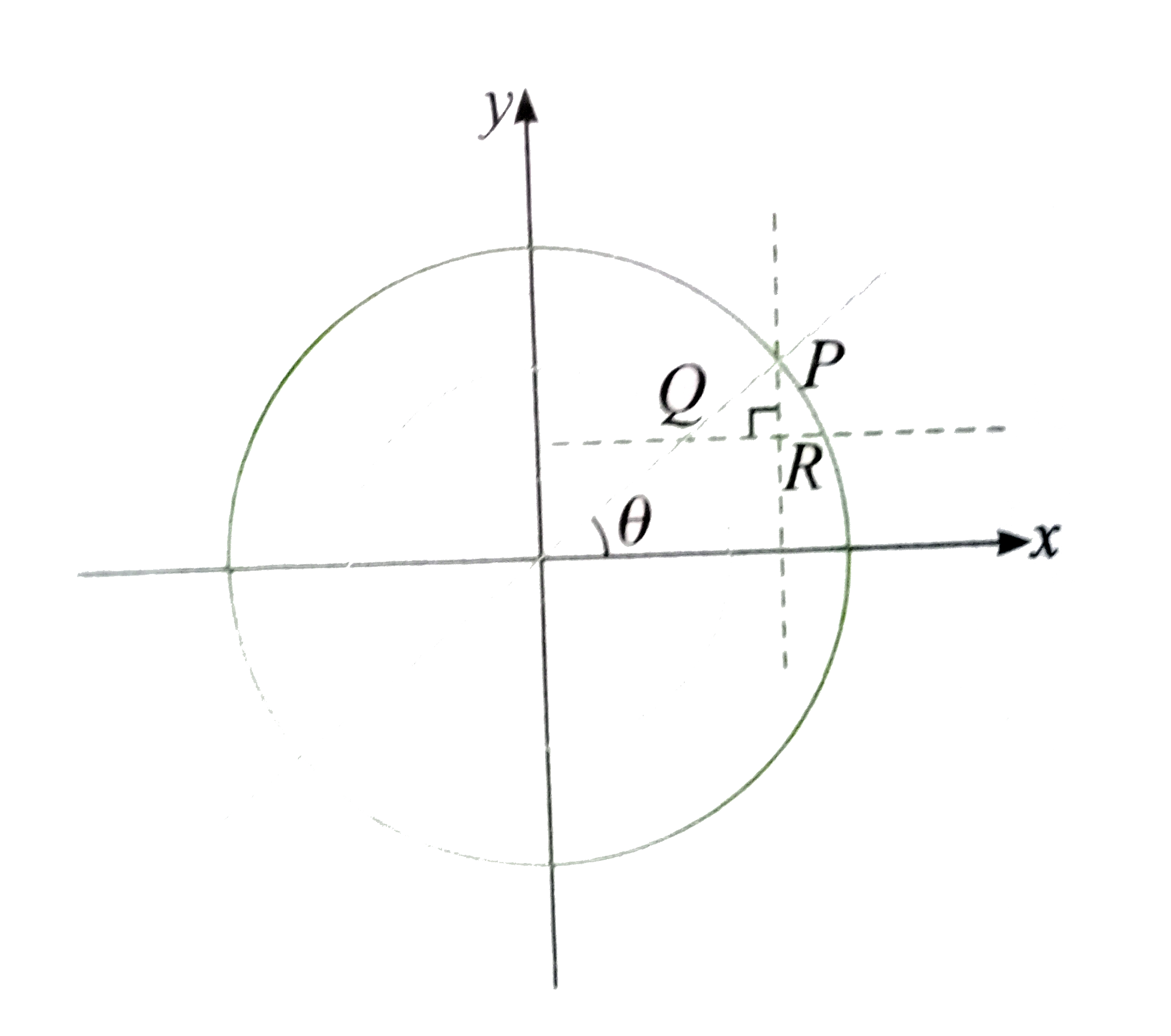
Squaring and adding, we get
So, is required locus.
Similar Questions
A line passing through the origin O(0,0) intersects two concentric circles of radii aandb at PandQ, If the lines parallel to the X-and Y-axes through QandP, respectively, meet at point R, then find the locus of R.
View SolutionThe line passing through the point of intersection of x+y=2,x−y=0 and is parallel to x+2y=5, is
View Solution
Knowledge Check
The line passing through the point of intersection of x+y=2, x-y=0 and is parallel to x+2y=5, is
Ax+2y=1Bx+2y=2Cx+2y=4Dx+2y=3A circle passes through the origin O and cuts the axes at A (a,0) and B (0,b). The image of origin O in the line AB is the point
A(2ab2a2+b2,2a2ba2+b2)B(2a2ba2+b2,2ab2a2+b2)C(2aba2+b2,2aba2+b2)D(a,b)
find equation of the line parallel to the line 3x−4y+2=0 and passing through the point (−2,3).
View SolutionFind the equation of the line parallel to the line 3x−4y+2=0 and passing through the point (−2,5).
View SolutionFind the equation of a line parallel to the line 3x−4y+2=0 and passing through the point. (−2,5).
View SolutionA point P moves on a plane xa+yb+zc=1. A plane through P and perpendicular to OP meets the coordinate axes at A,BandC. If the planes through A,BandC parallel to the planes x=0,y=0andz=0, respectively, intersect at Q, find the locus of Q.
View SolutionFind the equation of the line parallel to the y-axis and drawn through the point of intersection of the lines x−7y+15=0and2x+y=0.
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B.If the lines drawn parallel to axes through A and B meet at P then locus of P is
View Solution
