Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The angle between the tangents at A and C is
90∘
120∘
60∘
150∘
The correct Answer is:3
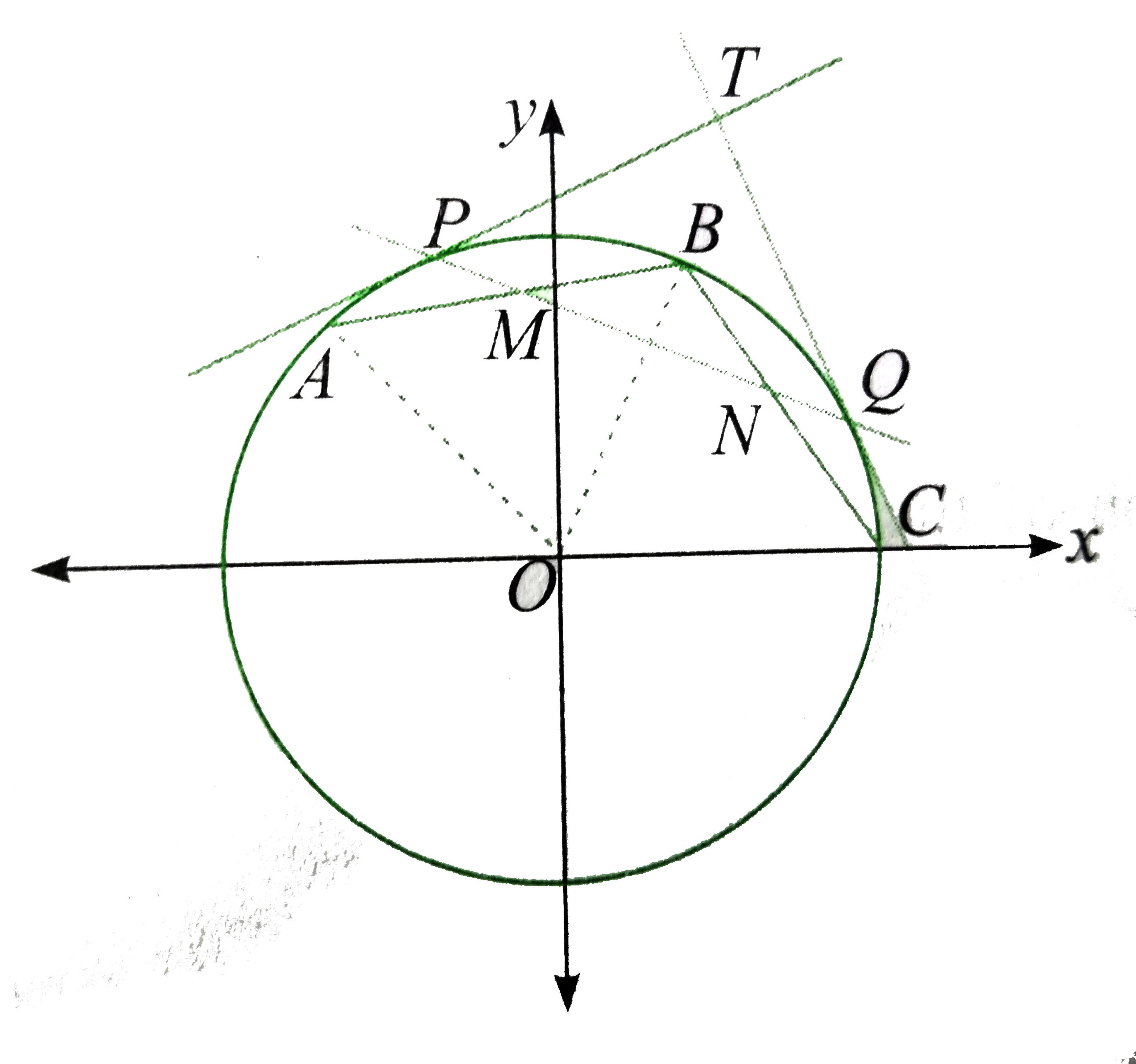
Let T be the point of intersection of tangents .
Since ∠AOC=120∘, the angle between the tangents is 60∘
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Video
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a ,then locus of point of intersection of tangents at A and C is a circle of radius λa, where λ is
View Solution
Knowledge Check
Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB isA30∘B60∘C45∘D15∘Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C isAx2+y2=a2Bx2+y2=2a2Cx2+y2=4a2Dx2+y2=8a2If ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
A4AC2B5AC2C54AC2D6AC2
ABCD is a square of area 1 m2. P and Q are the midpoints of AB and BC respectively. What is the area of Δ DPQ ?
View SolutionIn the figure, O is the center of the circle and BO is the bisector of angle ABC show that AB=BC
View SolutionAB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionB and C are points on the circle x2+y2=a2, A point A(b,c) lies on that circle such that AB=AC=d, the equation to BC is
View SolutionIn the given figure, M, N and P are the midpoints of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, then (BC + AC) - AB is
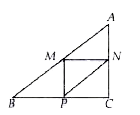
View Solution