Let C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
A
r,s,p,q
B
p,s,q,r
C
q,p,s,r
D
s,r,q,p
Video Solution
Text Solution
The correct Answer is:4
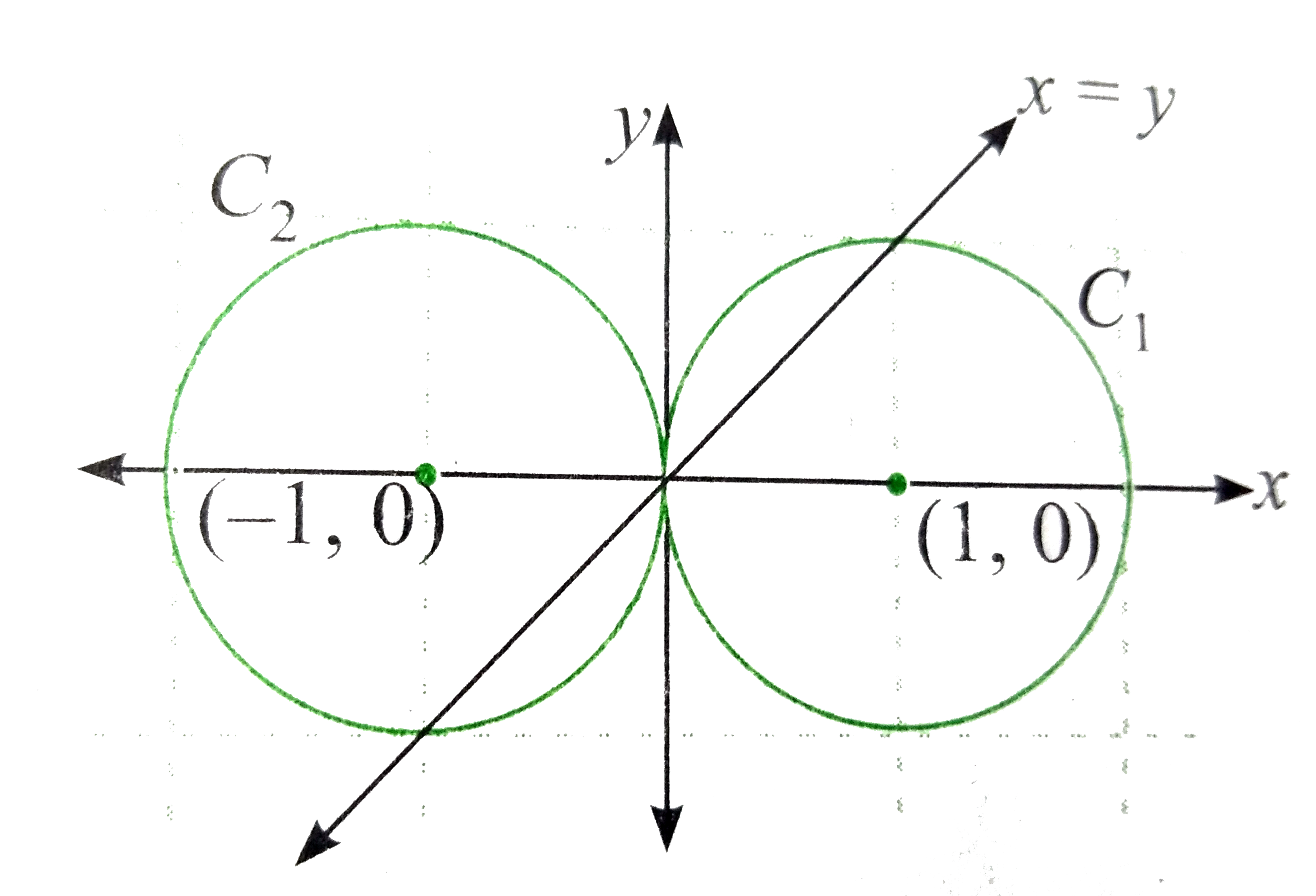
(λ,λ) lies on the line y=x ltbr> From the diagram, answer is (4)
|
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Numerical)
Explore 18 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:JEE Main Previous Year
Explore 10 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:MATRIX MATCH TYPE
Explore 6 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
Knowledge Check
Let C1andC2 be the circles x2+y2−2x−2y−2=0 and x2+y2−6x−6y+14=0 respectively. If P and Q are points of intersection of these circles, then the area (in sq. units ) of the quadrilateral PC1QC2 is :
A4B9C6D8The angle between x2+y2−2x−2y+1=0 and line y=λx+1−λ, is
A0∘B45∘C30∘D90∘Let C1andC2 be the centres of the circles x2+y2−2x−2y−2=0andx2+y2−6x+14=0 respectively. If P and Q are the points of intersection of these circles, then the area (in sq. units) of the quadrilateral PC1QC2 is:
A8B6C9D4
If the system of equations 2x−3y+4=0,5x−2y−1=0and21x−8y+λ=0 are consistent, then λ is
View SolutionIf (x+y)2=2(x2+y2) and (x–y+λ)2=4,λ>0, then λ is equal to
View SolutionThe equation of the circle which touches the axes of co-ordination and the line x3+y4=1 and when centre lines in the first quadrant is x2+y2−2λx−2λy+λ2=0, then λ is equal to :
View SolutionIf the equation x2+y2+6x−2y+(λ2+3λ+12)=0 represent a circle. Then
View SolutionThe equation of the circle whose diameter is the common chord of the circles x2+y2+2x+3y+2=0 and x2+y2+2x−3y−4=0 is
View Solution