Normal to the circle x2+y2=4 divides the circle having centre at (2,4) and radius 2 in the ares of ratio (π−2):(3π+2). Then the normal can be
A
y=x
B
y=3x
C
y=5x
D
y=7x
Video Solution
Text Solution
The correct Answer is:1,4
Normal to the circles x2+y2=4 passes through its centre (0,0)
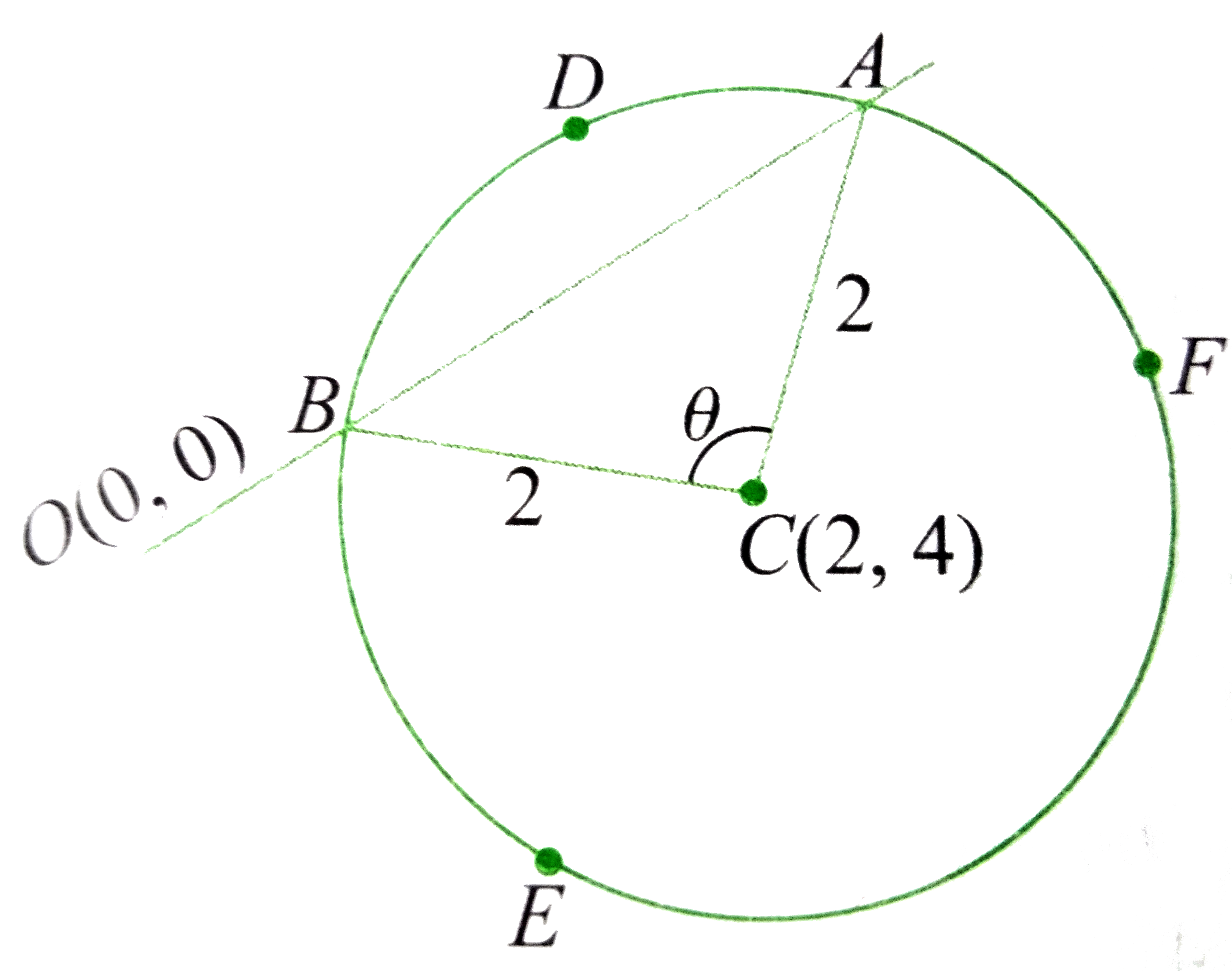
So, equation of normal is y=mx.
Now, according to the question.
Area of regio ADBAArea of regioN abefa=π−223π+2
∴[π(2)22π.θ−12(2)2sinθ]π(2)2−[π(2)22π.θ−12(2)2sinθ]=π−23π+2
⇒θ=π2
∴Distance of centre of circle from line =2cos.π4
⇒|4−2m|√1+m2=√2
⇒m=1,7
|
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Comprehension)
Explore 46 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:MATRIX MATCH TYPE
Explore 6 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Single)
Explore 109 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
Knowledge Check
The normal to the circle x2+y2−2x−2y=0 passing through (2,2) is
Ax=yB2x+y−6=0Cx+2y−6=0Dx+y−4=0The line 4x+3y-4=0 divides the circumference of the circle centred at (5,3) in the ratio 1:2. Then the equation of the circle is
Ax2+y2−10x−6y−66=0Bx2+y2−10x−6y+100=0Cx2+y2−10x−6y+66=0Dnone of theseRadius of the circle centred at (3,−2) , or maximum area contained in the circle x2+y2−4x+y=0 is
A(1/2)(√17−√13)B1/√2C√2Dnone of these
To the circle x2+y2+8x−4y+4=0 tangent at the point θ=π4 is
View SolutionLet the circle x2+y2=4 divide the area bounded by tangent and normal at (1,√3) and X-axis in A1andA2. Then A1A2 equals to
View SolutionIf one of the diameters of the circle x2+y2−2x−6y+6=0 is a chord to the circle with centre (2, 1), then the radius of circle is:
View SolutionThe circle x2+y2=4a2 is divided into two parts by the line x=3a2. Find the ratio of areas of these two parts.
View SolutionThe radius of a circle touching x-axis and having centre (2, 4) is
View Solution
