Question

The area of a rhombus is $480c{m}^2$ and the length of one of its diagonals is 20 cm . The length of each side of the rhombus is

Options

A. 24 cm
B. 30cm
C. 26 cm
D. 28 cm

Answer

C

Explanation

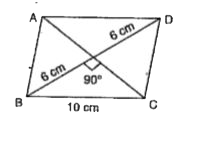
To find the length of each side of the rhombus given the area and one diagonal, we can follow these steps:

1. Understand the Given Information:
- Area of the rhombus (A) = 480 cm²
- Length of one diagonal (BD) = 20 cm

2. Use the Area Formula for a Rhombus:
The area of a rhombus can be calculated using the formula:
\( A = \frac{1}{2} \times d_1 \times d_2 \)
where \(d_1\) and \(d_2\) are the lengths of the diagonals.

3. Substitute the Known Values:
Here, we know \(A = 480\) cm² and \(d_1 = 20\) cm (BD). We need to find \(d_2\) (AC).
\( 480 = \frac{1}{2} \times 20 \times d_2 \)

4. Solve for \(d_2\):
Multiply both sides by 2:
\( 960 = 20 \times d_2 \)
Now divide by 20:
\( d_2 = \frac{960}{20} = 48 \text{ cm} \)

5. Find the Lengths of the Halves of the Diagonals:
Since the diagonals bisect each other at right angles, we can find the lengths of the halves:
- Half of \(BD\) (OB) = \( \frac{20}{2} = 10 \text{ cm} \)
- Half of \(AC\) (OC) = \( \frac{48}{2} = 24 \text{ cm} \)

6. Use the Pythagorean Theorem:
In triangle BOC, we can apply the Pythagorean theorem to find the length of side BC (which is also the length of each side of the rhombus):
\( BC^2 = OB^2 + OC^2 \)
Substituting the known values:
\( BC^2 = 10^2 + 24^2 \)
\( BC^2 = 100 + 576 = 676 \)
\( BC = \sqrt{676} = 26 \text{ cm} \)

7. Conclusion:
Therefore, the length of each side of the rhombus is:
\( \text{Length of each side} = 26 \text{ cm} \)