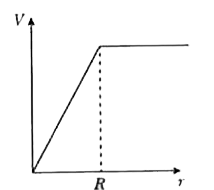
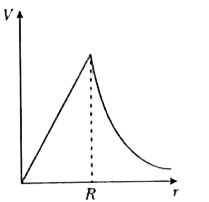
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by

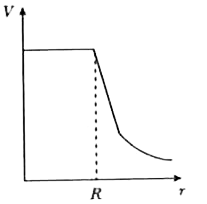
The correct Answer is:C
Step by step video, text & image solution for A spherically symmetric gravitational system of particles has a mass density rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):} whererho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0ltrltOO) form the centre of the system is represented by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)
6 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PROBLEMS
63 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)
4 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)
5 Videos
Similar Questions
The density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View Solution
Knowledge Check
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A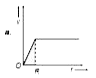 B
B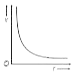 C
C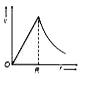 D
D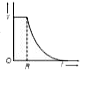
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A B
B C
C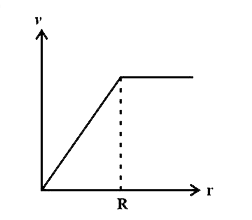 D
D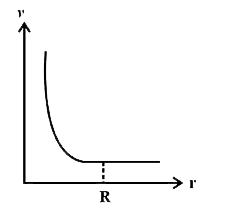
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A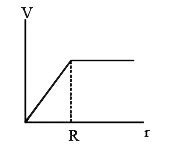 B
B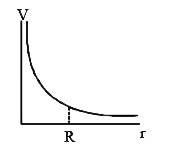 C
C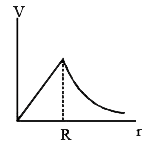 D
D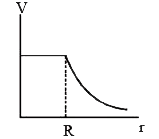
Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View SolutionA test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Identify the correct relation between the radius R of the particle’s orbit and its period T:
View SolutionThree particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionA test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Identify the correct relation between the radius R of the particle’s orbit and its period T:
View Solution
