In a pickup game of dorm shuffleboard, students crazed by final exams use a broom to propel a calculus book along the dorm hallway. If the 3.5 kg book is pushed from rest through a distance of 1.20 m by the horizontal 25 N force from the broom and then has a speed of 1.75 m/s, what is the coefficient of kinetic friction between the book and floor?
To find the coefficient of kinetic friction between the calculus book and the floor, we can follow these steps:
Step 1: Identify the known values
- Mass of the book, m=3.5kg
- Distance pushed, s=1.20m
- Applied force, F=25N
- Final speed, v=1.75m/s
- Initial speed, u=0m/s (since it starts from rest)
Step 2: Calculate the acceleration of the book
We can use the kinematic equation:
v2=u2+2as
Substituting the known values:
(1.75)2=02+2a(1.20)
3.0625=2.4a
a=3.06252.4≈1.276m/s2
Step 3: Apply Newton's second law
The net force acting on the book can be expressed as:
Fnet=F−Fk
Where Fk is the kinetic friction force. According to Newton's second law:
Fnet=ma
Thus, we have:
F−Fk=ma
Substituting the known values:
25−Fk=3.5×1.276
Calculating the right side:
25−Fk=4.466
Fk=25−4.466≈20.534N
Step 4: Relate the friction force to the coefficient of kinetic friction
The kinetic friction force can be expressed as:
Fk=μk⋅N
Where N is the normal force. Since the book is on a horizontal surface:
N=mg=3.5×9.8≈34.3N
Now substituting for Fk:
20.534=μk⋅34.3
Solving for μk:
μk=20.53434.3≈0.5986
Step 5: Round the answer
Thus, the coefficient of kinetic friction is approximately:
μk≈0.6
Final Answer:
The coefficient of kinetic friction between the book and the floor is approximately μk=0.6.
---
- Mass of the book, m=3.5kg
- Distance pushed, s=1.20m
- Applied force, F=25N
- Final speed, v=1.75m/s
- Initial speed, u=0m/s (since it starts from rest)
We can use the kinematic equation:
v2=u2+2as
Substituting the known values:
(1.75)2=02+2a(1.20)
3.0625=2.4a
a=3.06252.4≈1.276m/s2
The net force acting on the book can be expressed as:
Fnet=F−Fk
Where Fk is the kinetic friction force. According to Newton's second law:
Fnet=ma
Thus, we have:
F−Fk=ma
Substituting the known values:
25−Fk=3.5×1.276
Calculating the right side:
25−Fk=4.466
Fk=25−4.466≈20.534N
The kinetic friction force can be expressed as:
Fk=μk⋅N
Where N is the normal force. Since the book is on a horizontal surface:
N=mg=3.5×9.8≈34.3N
Now substituting for Fk:
20.534=μk⋅34.3
Solving for μk:
μk=20.53434.3≈0.5986
Thus, the coefficient of kinetic friction is approximately:
μk≈0.6
The coefficient of kinetic friction between the book and the floor is approximately μk=0.6.
Topper's Solved these Questions
- FORCE AND MOTION-IIBook:RESNICK AND HALLIDAYChapter:FORCE AND MOTION-IIExercise:PRACTICE QUESTIONS (Single Correct Choice Type)
Explore 23 Videos
- FORCE AND MOTION-IIBook:RESNICK AND HALLIDAYChapter:FORCE AND MOTION-IIExercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 4 Videos
- FORCE AND MOTION-IIBook:RESNICK AND HALLIDAYChapter:FORCE AND MOTION-IIExercise:CHECKPOINTS
Explore 5 Videos
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PRACTICE QUESTIONS (Integer Type)
Explore 3 Videos
- GAUSS' LAW Book:RESNICK AND HALLIDAYChapter:GAUSS' LAW Exercise:PRACTICE QUESTIONS (INTEGER TYPE)
Explore 3 Videos
Similar Questions
When the three blocks in Fig. 6-45 are released from rest, they accelerate with a magnitude of 0.500 m/s2 Block 1 has mass M, block 2 has 2M, and block 3 has 2M. What is the coefficient of kinetic friction between block 2 and the table?
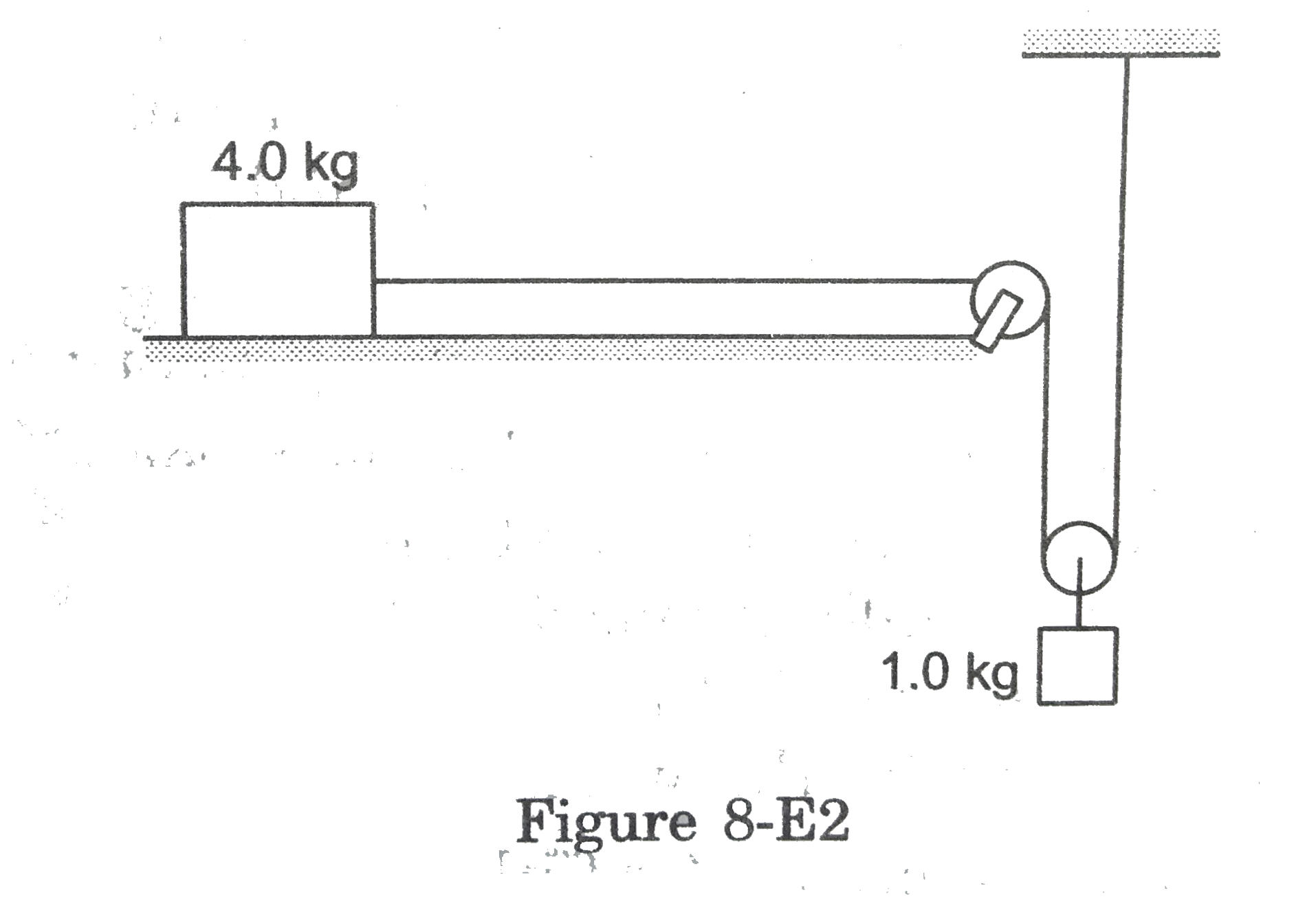
View SolutionConsider the situatioin shown in figure. The system is released from rest and the block of mass 1.0 kg is found to have a speed 0.3 m/s ater it has descended thrugh a distance of 1 m. find the coefficient of kinetic friction between the block and the table.
View Solution
Knowledge Check
A 30kg block rests on a rough horizontal surface A force of 200N is applied on the block The block acquires a speed of 4m/s starting from rest in 2s What is the value of coefficient of friction ? .
A√3/10B10/3C0.47D0.185A block with mass 0.50kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20m (figure). When released, the block moves on a horizontal table top for 1.00N/m. What is the coefficient of kinetic friction μk, between the block and the block and the table?
 A0.40B0.50C0.25Dnone of these
A0.40B0.50C0.25Dnone of theseA body of mass 5 kg rests on a rough horizontal surface of coefficient of friction 0.2. The body is pulled through a distance of 10 m by a horizontal force of 25 N . The kinetic energy acquired by it is (g=10ms2)
A330JB150JC100JD50J
A boy is sitting on the horizontal platform of a joy wheel at a distance of 5 m from the center. The wheel begins to rotate and when angular speed exceeds 1 rad/s, the boy just slips. The coefficient of friction between the boy and the wheel is (g=10m/s2)
View SolutionA 4.10 kg block is pushed along a floor by a constant applied force that is horizontal and has a magnitude of 50.0 N. Figure 6-46 gives the block's speed v versus time t as the block moves 0.5 1.0 along an x axis on the floor. The scale of the figure's vertical axis is set by vs=5.0 m/s. What is the coefficient of kinetic friction between the block and the floor?

View SolutionA 4.00g bullet travelling horizontally with a velocity of magnitude 500m/s is fired into a wooden block with a mass of 1.00kg, initially at rest on a level surface. The bullet passes through the block and emerges with speed 100m/s. The block slides a distance of 0.30m along the surface from its initial position.
(a) What is the coefficient of kinetic friction between block and surface?
(b) What is the decrease in kinetic energy of the bullet?
(c) What is the kinetic energy of the block at the instant after the bullet has passed through it? Neglect friction during collision of bullet with the block.
View SolutionYou push a 2.0 kg block against a horizontal spring , compressing the spring by 12 cm. Then You release the block, and the spring sends it sliding across a tabletop. It stops 75 cm from where you released it. The spring constant is 170 N/m. What is the block-table coefficient of kinetic friction ?
View SolutionA flat bottomed metal tank of water is dragged along a horizontal floor at the rate of 20ms−1. The tank is of mass 20kg and contains 1000 kg of water and all the heat produced in the dragging is conducted to the water through the bottom plate of the tank. If the bottom plate has an effective area of conduction 1 m^2 and a thickness 5 cm and the temperature of the water in the tank remains constant at 50∘C, calculate the temperature of the bottom surface of the tank, given the coefficient of friction between the tank and the floor is 0.343 and K for the material of the tank is 25calm−1s−1K−1.
View Solution

