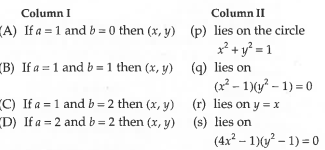Let (x,y) be such that sin−1(ax)+cos−1(bxy)=π2 If a=1andb=0, then (x,y)
Column I Column IIA.ifa=1andb=0, then (x,y)p. lies on the circle x2+y2=1
Column I Column IIB.ifa=1andb=1, then(x,y)q.lies on (x2−1)(y2−1)
Column I Column IIC.ifa=1andb=2, then (x,y)r.lies on y=x
Column I Column IID.ifa=2andb=2, then (x,y)s.lies on (4x2−1)(y2−1)
The correct Answer is:A, B, C, D
A. If a=1,b=0, then sin−1x+cos−1y=0
⇒sin−1x=−cos−1y⇒x2+y2=1
B. If a=1andb=1, then
sin−1x+cos−1y+cos−1xy=π2
⇒cos−1x−cos−1y=cos−1xy
⇒xy+√1−x2√1−y2=xy⇒(x2−1)(y2−1)=0
C. If a=1,b=2, then
sin−1x+cos−1y+cos−1(2xy)=π2
⇒cos−1x−cos−1y=cos−1(2xy)
⇒xy+√1−x2√1−y2=2xy⇒x2+y2=1
D. If a=2andb=2, then
sin−1(2x)+cos−1(y)+cos−1(2xy)=π2
⇒cos−1(2x)−cos−1(y)=cos−1(2xy)
⇒2xy+√1−4x2√1−y2=2xy
⇒(4x2−1)(y2−1)=0
Topper's Solved these Questions
- INVERSE CIRCULAR FUNCTIONS Book:IIT JEE PREVIOUS YEARChapter:INVERSE CIRCULAR FUNCTIONS Exercise:PROPERTIES OF INVERSE FUNCTIONS (NUMERICAL VALUE BASED)
Explore 1 Video
- INVERSE CIRCULAR FUNCTIONS Book:IIT JEE PREVIOUS YEARChapter:INVERSE CIRCULAR FUNCTIONS Exercise:PROPERTIES OF INVERSE FUNCTIONS ( ANALYTICAL & DESCRIPTIVE QUESTION)
Explore 2 Videos
- INVERSE CIRCULAR FUNCTIONS Book:IIT JEE PREVIOUS YEARChapter:INVERSE CIRCULAR FUNCTIONS Exercise:PROPERTIES OF INVERSE FUNCTIONS (OBJECTIVE QUESTIONS II)
Explore 8 Videos
- INDEFINITE INTEGRATIONBook:IIT JEE PREVIOUS YEARChapter:INDEFINITE INTEGRATIONExercise:IRRATIONAL FUNCTION & PARTIAL FRACTION
Explore 4 Videos
- JEE MAINSBook:IIT JEE PREVIOUS YEARChapter:JEE MAINSExercise:All Questions
Explore 1 Video
Similar Questions
Knowledge Check
Let (x,y)be such that
sin−1(ax)+cos−1y+cos−1(bxy)=π2
If a=1 alnd b=2 then (x,y)lies onAx2+y2=1B(x2−1)(y2−1)=0Cy=xD(4x2−1)(y2−1)=0If sin−1x+sin−1y=π2andsin2x=cos2y, then
Ax=π8+√12−π264By=√12−π264−π12Cx=π12+√12−π264Dy=√12−π264−π8If sin−1x+sin−1y=2π3andcos−1x−cos−1y=π3, then (x,y)=
A(1,1)B(12,1)C(1,12)D(13,13)
Let x y be such that (x−y)∈(π3π) If sinx+siny=−2165 and cosx+cosy=−2765 then cos(x−y2) is equal
View SolutionLet x y be such that (x−y)∈(π,3π) If sinx+siny=−2165 and cosx+cosy=−2765 then cos(x−y2) is equal
View SolutionLet x y be such that (x−y)∈(π3π) .If sinx+siny=−2165 and cosx+cosy=−2765 then cos(x−y2) is equal
View SolutionIf cos(x−y)=−1, show that cosx+cosy=0 and sinx+siny=0.
View SolutionIf −1≤x,y≤1 such that sin−1x+sin−1y=2π3, find the value of cos−1x+cos−1y.
View Solution