Doubtnut Promotions Sticky

If 0<x<1, then √1+x2[{xcos(cot−1x)+sin(cot−1x)}2−1]12 is equal to

A

x√1+x2

B

x

C

x√1+x2

D

√1+x2

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

We have, 0<x<1
Let cot−1x=θ
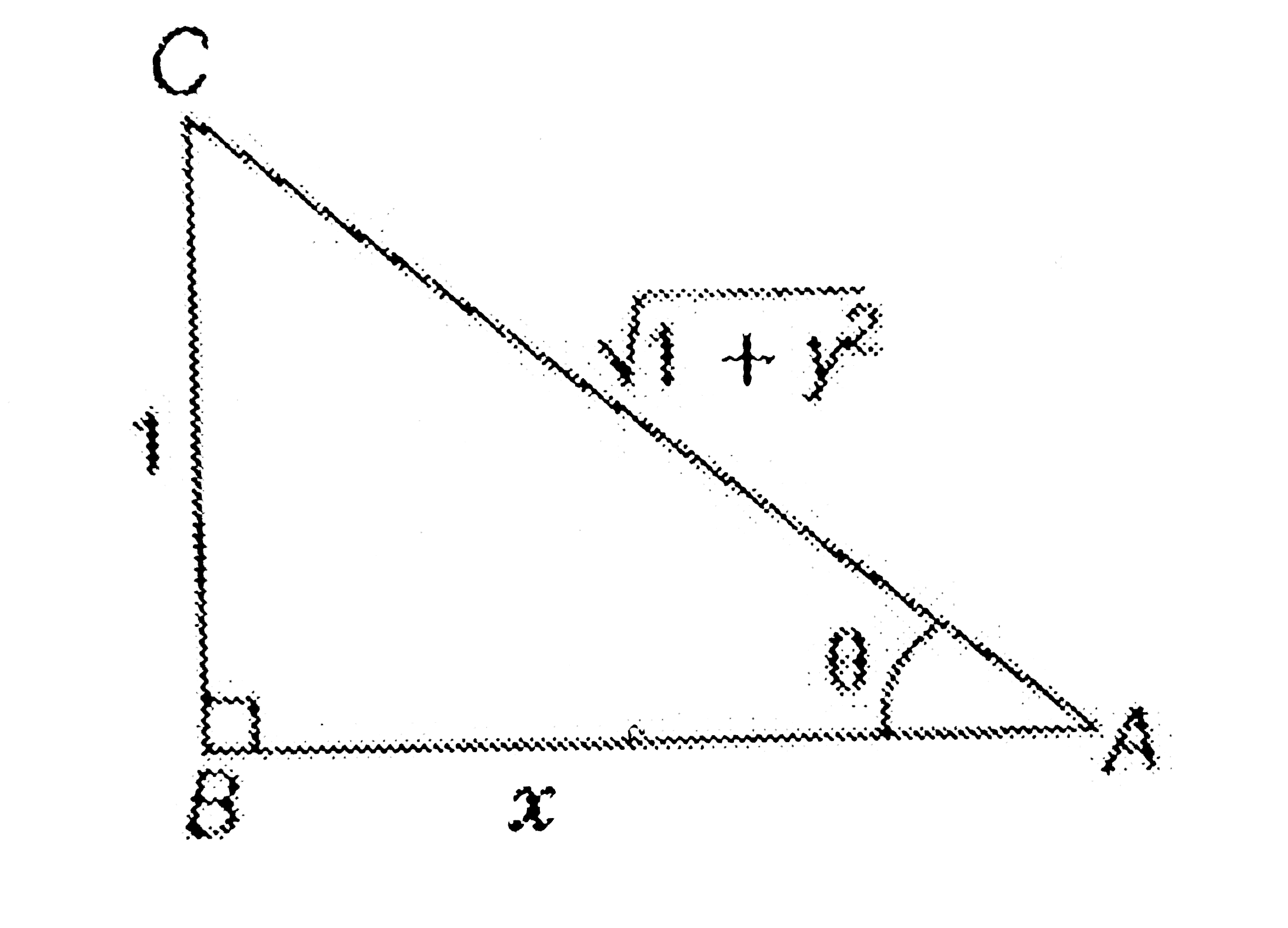
ocr_image
⇒ cotθ=x
⇒ sinθ=1√1+x2=sin(cot−1x)
and cotθ=x√1+x2=cos(cot−1x)
Now, √1+x2[{xcos(cot−1x)+sin(cot−1x)}2−1]1/2
=√1+x2⎡⎣(x−x√1+x2+1√1+x2)2−1⎤⎦1/2
=√1+x2⎡⎣(1+x2√1+x2)2−1⎤⎦1/2
=√1+x2[1+x2−1]1/2=x√1+x2

|
Updated on:21/07/2023
Class 12MATHSFUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    If A = ⎡⎢⎣000000010⎤⎥⎦ ,then A is

    Aan invertible matrix
    Ban idenpotent matrix
    Ca nilpotent matrix
    Dnone of these
  • Question 2 - Select One

    If A = ⎡⎢⎣000100010⎤⎥⎦ ,then

    AA2=A
    BA2=0
    CA2=I
    DA3=O
  • Question 3 - Select One

    If A=⎡⎢⎣200020002⎤⎥⎦, then A6= .........

    A6A
    B12A
    C16A
    D32A.