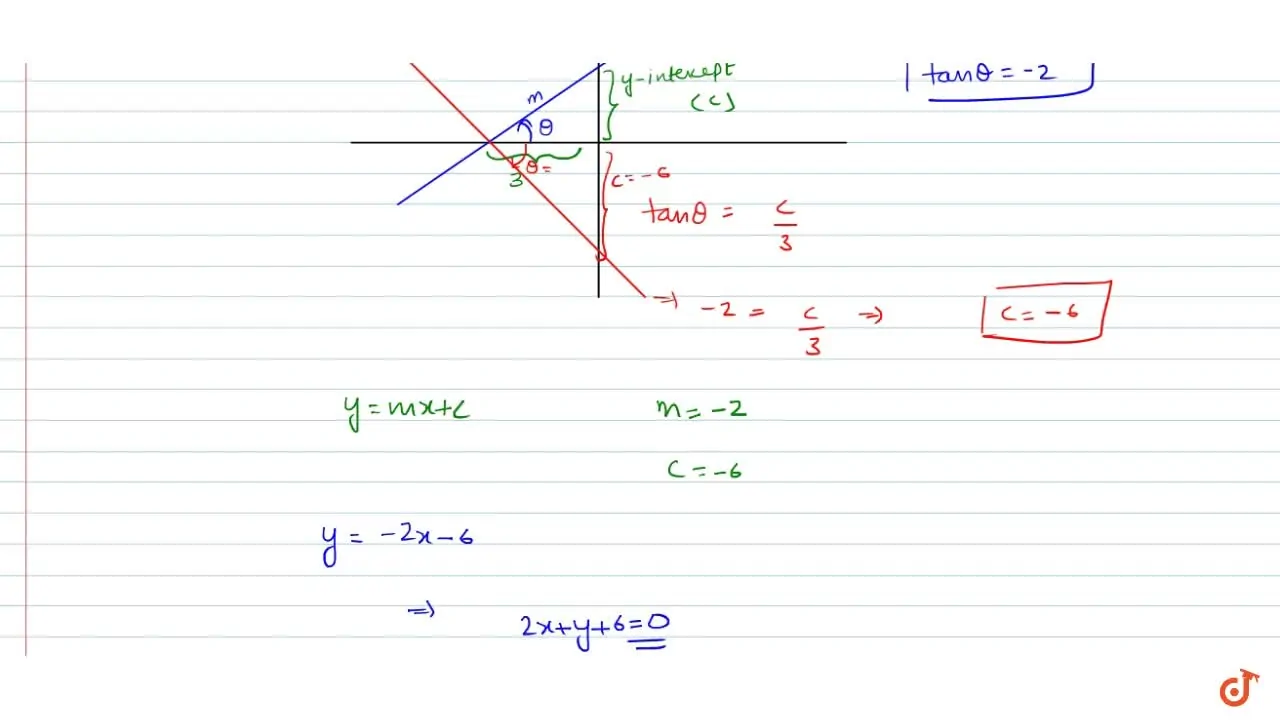
Find the equation of a straight line: with slope -2 and intersecting the x-axis at a distance of 3 units to the left of origin.
We know that the equation of a line with slope m and x-intercept d is given by y=m(x-d).
Here, m=-2 and d=-3
Hence, the required equation of the line is
y=−2(x+3)⇒2x+y+6=0
Related Playlists
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - SOLVED-EXAMPLE12videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - MISCELLANEOUS PROBLEMS9videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - EXERCISE 20K10videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STATISTICSEXERCISE - EXERCISE 30D5videos
STATISTICS
- BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 26 C13videos
THREE-DIMENSIONAL GEOMETRY
Similar Questions
Find the equation of a straight line: with slope 2 and y-intercept 3;
View SolutionFind the equation of a straight line: with slope -1/3 and y-intercept -4.
View SolutionFind the equation of the line which satisfy the given conditions : Intersecting the xaxis at a distance of 3 units to the left of origin with slope 2.
View SolutionFind the equation of the straight lines which are : parallel to the x-axis at a distance of 5 units from it
View SolutionFind the equation of the line with slope 23 and intercept on the y-axis is 5 :
View SolutionFind the equation of the line which satisfy the given conditions : Intersecting the yaxis at a distance of 2 units above the origin and making an angle of 30∘with positive direction of the xaxis.
View SolutionFind the equation of the line intersecting x-axis at a distance of 3 units to the left of the origin with slope −2.
View SolutionFind the equation of a line whose slope is 3 intersects X-axis on left side at a distance of 2 untis from origin.
View SolutionFind the equation of the line passing through (0,2) making an angle 2π3 with the positive X-axis. Also find the equation of the line parallel to it and crossing the Y-axis at a distance of two units below the origin.
View SolutionWhich of the following will be the equation of a straight line parallel to the y-axis at a distance of 9 units to the left?
View Solution