Question

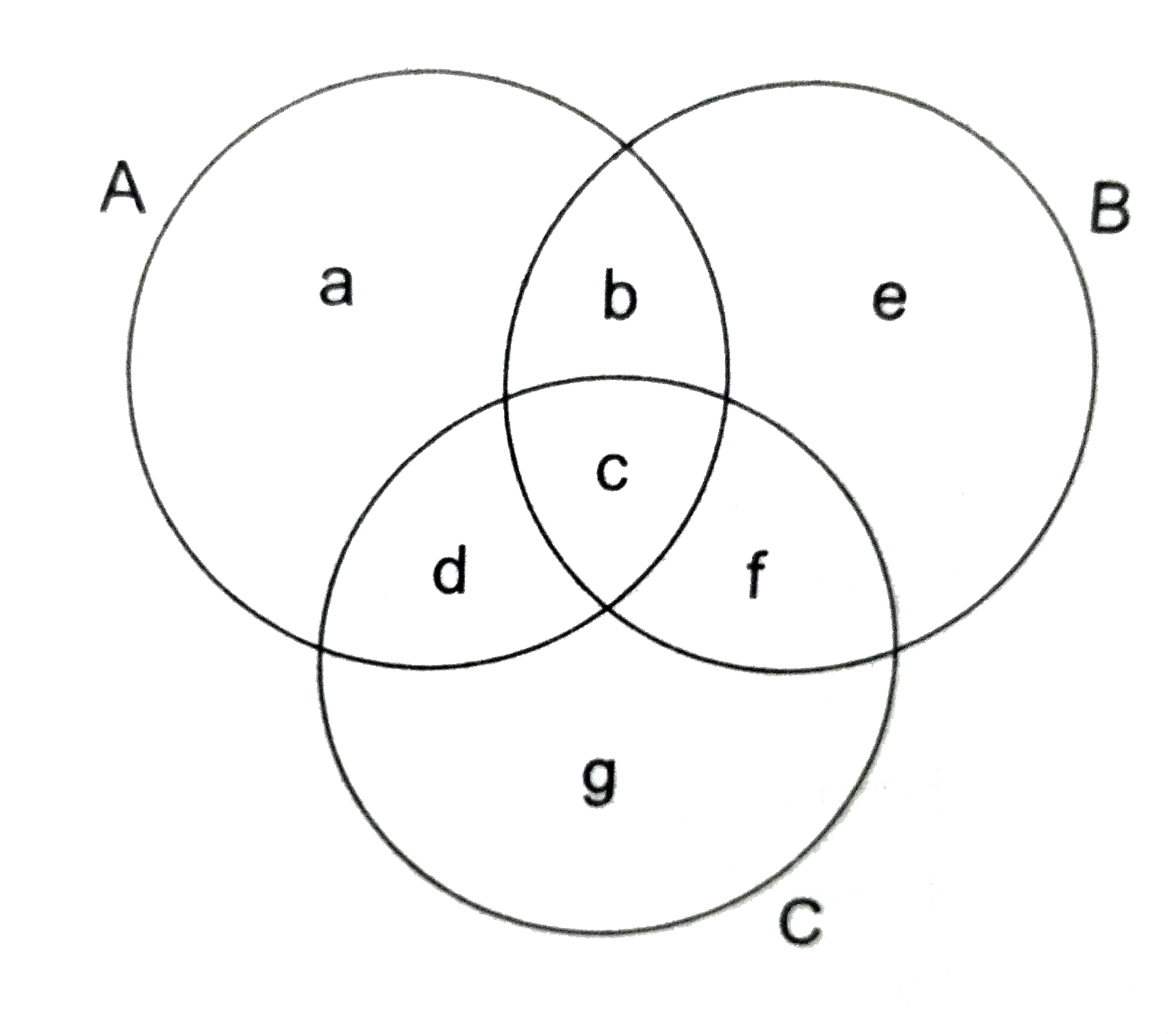
In a town of $10,000$ families, it was found that $40\%$ of the families buy newspaper $A$, $20\%$ buy newspaper $B$, $10\%$ buy newspaper $C$, $5\%$ buy $A$ and $B$, $30\%$ buy $B$ and $C$ and $4\%$ buy $A$ and $C$. If $2\%$ buy all the three newspapers, find the number of families which buy.
(i) A only,
(ii) B only,
(iii) none of A, B and C.

Answer

(i) `3300`
(ii) `1400`
(iii) `4000`

Explanation

`n(A) =(40% of 10000) =((40)/(100) xx10000)=40000`,
` n(B) =(20% Of 10000)=2000, n(C) =(10%of 10000) =1000`,
`n( A cap B) =(5% of 10000)= 500, n( B cap C)= (3% of 10000) =300`,
` n( A cap C) =(4% of 10000) =4000, n(A cap B cap C) =(2% of 10000) =200`,
and ` n(U) =10000`,
`{(a+b+c+d,=4000","),(b+c+e+f,=2000","),(c+d+f+g,=1000","),(" "b+c,=500","),(" "c+f,=300","),(" "c+d,=400","),(" "c,=200","):}`