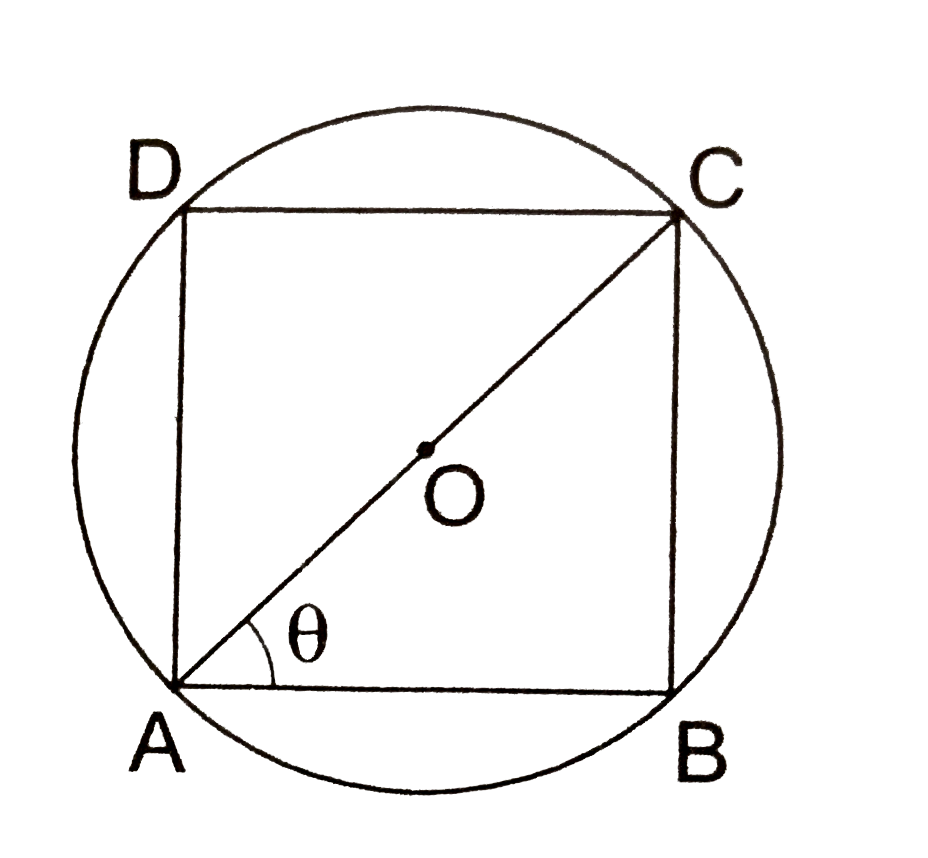
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.

Video Solution

Text Solution

Verified by Experts

Let ABCD be a rectangle inscribed in a given circle with centre O and radius r.
Let $a n l \geq C A B = θ$
The, $A C = 2 r, A B = 2 r cos θ and B C = 2 r sin θ$
Let A be the area of rectangel ABCD.
The, $A = A B \times B C = 4 r^{2} sin θ cos θ = 2 r^{2} sin 2 θ$
Thus, $A = 2 r^{2} sin, 2 θ$ , where r is constant
$∴ \frac{d A}{d θ} = 4 r^{2} cos 2 θ and \frac{d^{2} A}{d θ^{2}} = - 8 r^{2} sin 2 θ$
Now, $\frac{d A}{d θ} = 0 \Rightarrow 4 r^{2} cos 2 θ = 0 \Rightarrow cos 2 θ = 0 \Rightarrow 2 θ = \frac{π}{2}, i.e., θ = \frac{π}{4}$
And, $[\frac{d^{2} A}{d t h η^{2}}] = - 8 r^{2} sin \frac{π}{2} = - 8 r^{2} < 0$
$∴ θ = (π / 4)$ is a point of maximum.
Thus, area is maximum when $θ = (π / 4)$
In this case, $A B = 2 r cos \frac{π}{4} = r \sqrt{2}$
and, $B C = 2 r sin \frac{π}{4} = r \sqrt{2}$
Thus, $A B = B C$ and therefore, ABCD is a square.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-APPLICATIONS OF DERIVATIVES-Objective Questions

Home
Ask Doubt
Profile