Prove that the area of right-angled triangle of given hypotenuse is maximum when the triangle is isosceles.

Video Solution

Text Solution

Verified by Experts

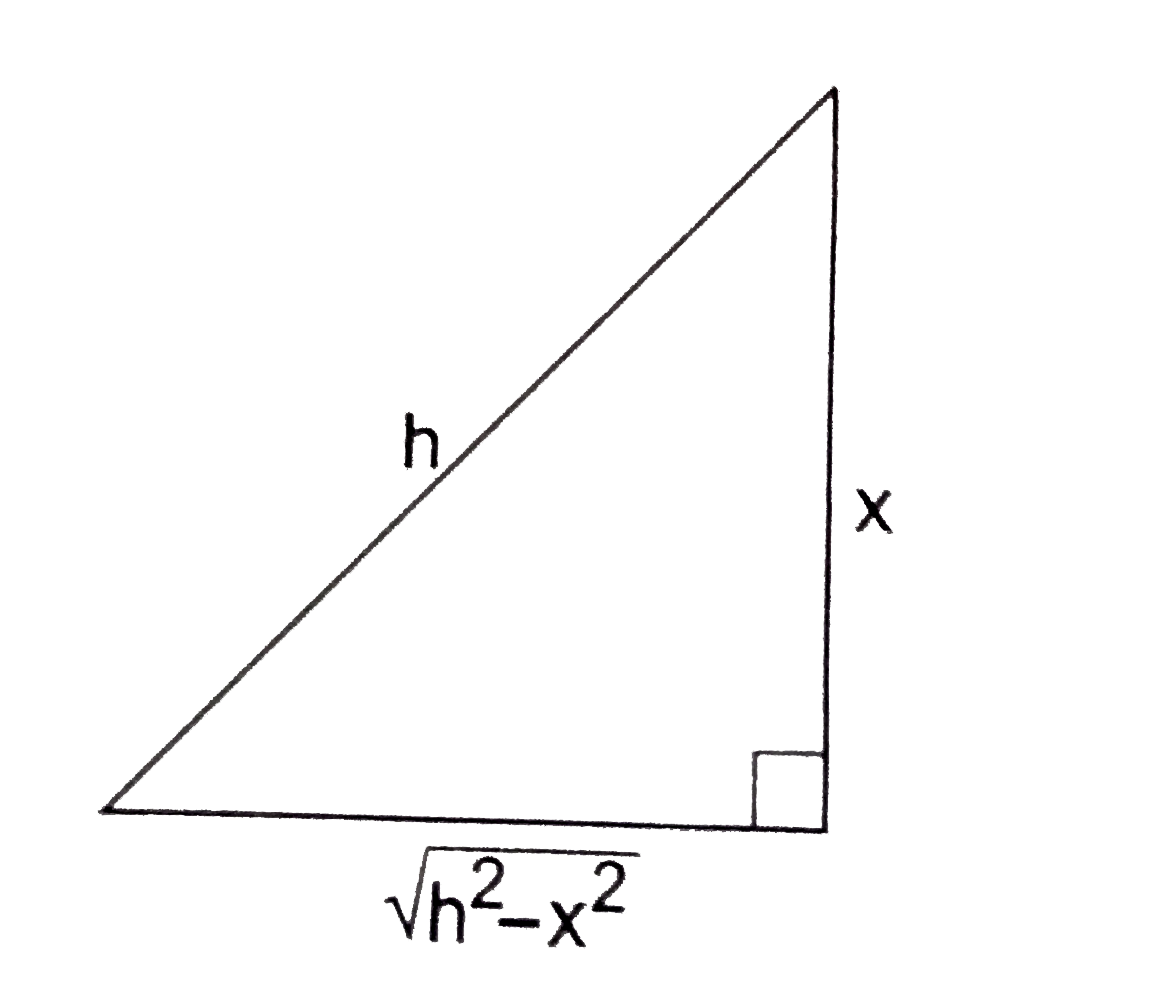
Let h be the hypotenuse of the triangle and x be its altitude.
The, the base of the triangle $= \sqrt{b^{2} - x^{2}}$
Now, $A = \frac{1}{2} x \sqrt{h^{2} - x^{2}}$
$∴ \frac{d A}{d x} = \frac{1}{2} {x . \frac{1}{2} {(h^{2} - x^{2})}^{- 1 / 2} (- 2 x) + \sqrt{h^{2} - x^{2}}}$
$= \frac{1}{2} (\frac{h^{2} - 2 x^{2}}{\sqrt{h^{2} - x^{2}}})$
and, $\frac{d^{2} A}{{d x}^{2}} = \frac{(\sqrt{h^{2} - x^{2}}) (- 4 x) - (h^{2} - 2 x^{2}) . \frac{1}{2} {(h^{2} - x^{2})}^{- 1 / 2} (- 2 x)}{2 (h^{2} - x^{2})}$
$= \frac{(2 x^{3} - 3 x h^{2})}{2 {(h^{2} - x^{2})}^{3 / 2}}$
Now, $\frac{d A}{d x} = 0 \Rightarrow (h^{2} - 2 x^{2}) = 0 \Rightarrow x = \frac{h}{\sqrt{2}}$
$∴ {[\frac{d^{2} A}{{d x}^{2}}]}_{x = \frac{h}{\sqrt{2}}} = - 2 < 0$
Thus, A is maximum at $x = (h / \sqrt{2})$
$∴$ base $= \sqrt{h^{2} - x^{2}} = \sqrt{(h^{2} - \frac{h^{2}}{2})} = \frac{h}{\sqrt{2}} =$ altitude
Hence, the triangle is isosceles

Updated on:21/07/2023