If f be a greatest integer function and g be an absolute value functio

If f be greatest integer function defined asf(x)=[x] and g be the mdoulus function defined as g(x)=|x|, then the value of g of $(- \frac{5}{4})$ is _____
A-1
B0
C1
D2
If f be the greatest integer function and g be the moduls function, then $(g o f) (- \frac{5}{2}) - (f o g) (- \frac{5}{3}) =$
A1
B $- 1$
C2
D4
Let f(x) be the greatest integer function and g(x) be the modulus function.
What is $(g o f) (- \frac{5}{3}) - (f o g) (- \frac{5}{3})$ equal to?
A $- 1$
B0
C1
D2

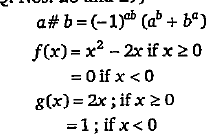
If $f$ be a greatest integer function and $g$ be an absolute value function, find the value of $(f \circ g) (- \frac{3}{2}) + (g \circ f) (\frac{4}{3}) .$