Define a functions . What do you mean by the domain and range of a function ? Give examples.
Step-by-Step Solution:
Step 1: Define a Function
A function is a special type of relation between two sets, typically referred to as the domain and the codomain. In a function, each element in the domain (input) is associated with exactly one element in the codomain (output). This means that for every input value, there is a unique output value.
Example of a Function:
Let’s consider two sets:
- Set A (Domain): {1, 2, 3, 4, 5}
- Set B (Codomain): {A, B, C, D, E, F}
A possible function can be defined as follows:
- f(1) = A
- f(2) = B
- f(3) = C
- f(4) = D
- f(5) = E
In this case, every element from Set A has a unique corresponding element in Set B.
---
Step 2: Define Domain
The domain of a function is the complete set of possible values of the independent variable (input). It consists of all the values that can be input into the function.
Example of Domain:
For the function defined above, the domain is:
- Domain: {1, 2, 3, 4, 5}
---
Step 3: Define Range
The range of a function is the set of all output values (dependent variable) that the function can produce. It consists of all the values that are actually output from the function.
Example of Range:
From our function example, the outputs are:
- Range: {A, B, C, D, E}
---
Step 4: Define Co-domain
The co-domain is the set of all potential outputs of the function, which includes all the values that could possibly be output, even if they are not actually produced by the function.
Example of Co-domain:
In our example, the co-domain is:
- Co-domain: {A, B, C, D, E, F}
---
Summary:
- Function: A relation where each input has a unique output.
- Domain: The set of all possible inputs.
- Range: The set of actual outputs produced by the function.
- Co-domain: The set of all potential outputs.
A function is a special type of relation between two sets, typically referred to as the domain and the codomain. In a function, each element in the domain (input) is associated with exactly one element in the codomain (output). This means that for every input value, there is a unique output value.
Let’s consider two sets:
- Set A (Domain): {1, 2, 3, 4, 5}
- Set B (Codomain): {A, B, C, D, E, F}
- f(1) = A
- f(2) = B
- f(3) = C
- f(4) = D
- f(5) = E
The domain of a function is the complete set of possible values of the independent variable (input). It consists of all the values that can be input into the function.
For the function defined above, the domain is:
- Domain: {1, 2, 3, 4, 5}
The range of a function is the set of all output values (dependent variable) that the function can produce. It consists of all the values that are actually output from the function.
From our function example, the outputs are:
- Range: {A, B, C, D, E}
The co-domain is the set of all potential outputs of the function, which includes all the values that could possibly be output, even if they are not actually produced by the function.
In our example, the co-domain is:
- Co-domain: {A, B, C, D, E, F}
- Function: A relation where each input has a unique output.
- Domain: The set of all possible inputs.
- Range: The set of actual outputs produced by the function.
- Co-domain: The set of all potential outputs.
Topper's Solved these Questions
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - Exercise 2B
12 Videos
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - Exercise 2C
20 Videos
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - Objective Questions
39 Videos
- DIFFERENTIATIONBOOK - RS AGGARWALCHAPTER - DIFFERENTIATIONEXERCISE - Exercise 10I
51 Videos
- FUNDAMENTAL CONCEPTS OF 3-DIMENSIONAL GEOMETRYBOOK - RS AGGARWALCHAPTER - FUNDAMENTAL CONCEPTS OF 3-DIMENSIONAL GEOMETRYEXERCISE - Exercise
18 Videos
Similar Questions
Domain codomain and range of function
View SolutionRange and domain of a functions
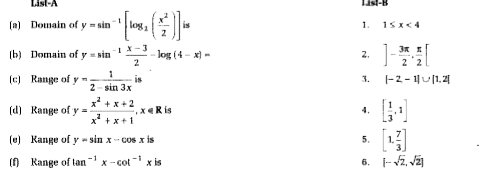
View SolutionWrite the domain and range of the signum function,
View SolutionWrite the domain and range of the function f(x)=[x]
View SolutionWhat do you mean by range of vision ?
View SolutionFunction and Domain , Codomain and Range of function
View SolutionLet A and B be two nonempty sets.
(i) What do you mean by a relation from A to B?
(ii) What do you mean by the domain and range of a relation?
View SolutionWhat do you mean by SCP? Give example.
View SolutionWhat is the domain and range of the function f(x)=1−|ln(|x|−1)|
View SolutionWrite the domain and the range of the function, f(x)=−|x|.
View Solution
