Sketch the graph of a function f that satifies the given values:
f(−2)=0 ,f(2)=0, limx→−2f(x)=0 , limx→2f(x) does not exist.Solution in Tamil
The correct Answer is:does not exist
Step by step video, text & image solution for Sketch the graph of a function f that satifies the given values: f(-2)=0 ,f(2)=0, lim_(x to -2) f(x)=0 , lim_(x to 2) f(x) does not exist. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - FULL MARKSCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.2
15 Videos
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - FULL MARKSCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.3
13 Videos
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - FULL MARKSCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - ADDITIONAL PROBLEMS
11 Videos
- DIFFERENTIAL CALCULUS - DIFFERENTIABILITY AND METHODS OF DIFFERENTIATIONBOOK - FULL MARKSCHAPTER - DIFFERENTIAL CALCULUS - DIFFERENTIABILITY AND METHODS OF DIFFERENTIATIONEXERCISE - EXERCISE 5 ADDITIONAL PROBLEMS (Find the derivative of following functions.)
10 Videos
- EXAMINATION QUESTION PAPER - JUNE 2019 BOOK - FULL MARKSCHAPTER - EXAMINATION QUESTION PAPER - JUNE 2019 EXERCISE - PART -IV
7 Videos
Similar Questions
Evaluate the limits :
limx→2x4−16x−2
View SolutionFind the left and right limits of f(x)=x2−4(x2+4x+4)(x+3) at x=−2.
View SolutionSuppose f(x)=⎧⎪⎨⎪⎩a+bxx<14x=1b−axx>1 and if limx→1f(x)=f(1). What are possible values of a and b?
View SolutionDifferentiate following as; 3sinx+4cosx−ex
View Solution(a) Let f,g : R→R be defined as f(x) =2x−|x| and g(x) =2x+|x|. Find fog.
(b) Prove that limθ→0sinθθ=1
View SolutionGiven lim_(x rarr0)(f(x))/(x^(2))=2 then lim_(x rarr0)[f(x)]=
View SolutionThe graph of y = f(x) is as shown in the following figure.
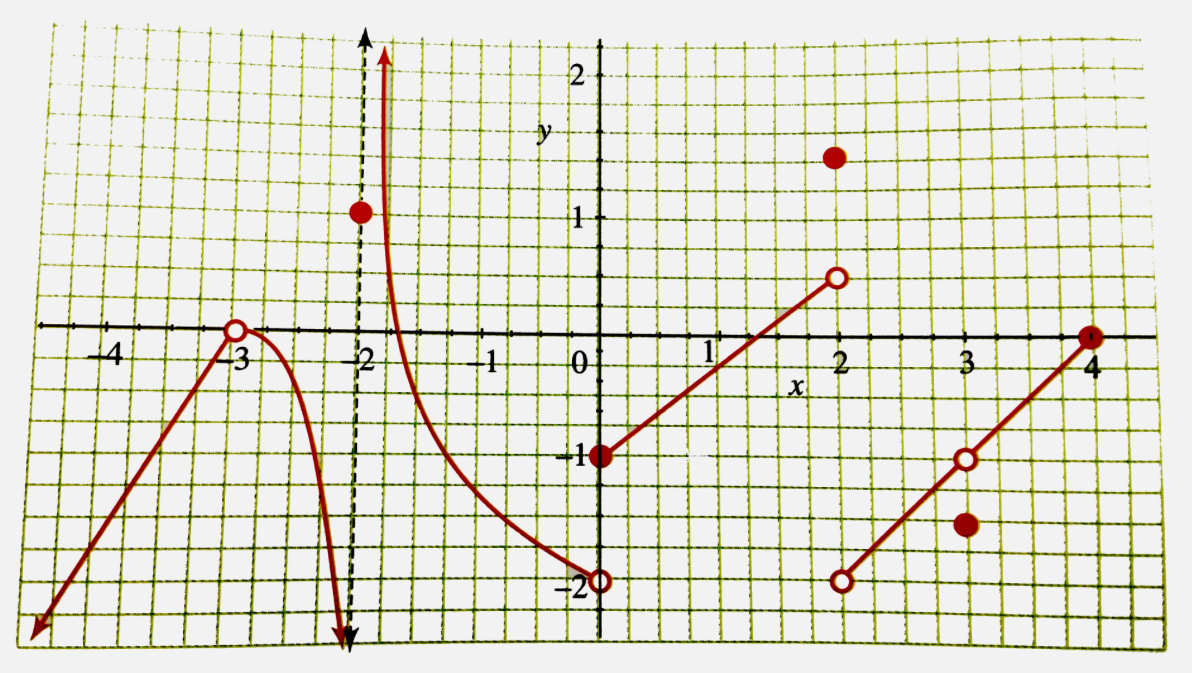
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionIf f(x)={x−|x|x,x≠02, x=0,show that limx→0f(x) does not exist.
View SolutionLet f(x)={|x|x,x≠02,x=0.
Show that limx→0f(x) does not exist.
View Solutionयदि f एक निरंतर वर्धमान फलन है तब limx→0f(x2)−f(x)f(x)−f(0) का मान है :
View Solutionयदि f एक फलां इस प्रकार है कि f(−x)=−f(x) तथा limx→0f(x) का अस्तित्व है तब सिद्ध कीजिए कि limx→0f(x)=0
View SolutionSketch the graph of a function f that satisfies the given values:
f(0) is underfined limx→0f(x)=4,
f(2) = 6, limx→2f(x)=3
View SolutionSketch the graph of a function f that satisfies the given values:
f(-2) = 0 , f(2) = 0 , limx→−2f(x)=0
limx→2f(x) does not exist.
View SolutionSketch the graph of a function f that satifies the given values:
f(0) is undefined limx→0f(x)=4, f(2)=6 , limx→2f(x)=3
View SolutionThe graph of y = f(x) is as shown in the following figure.

Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View Solution
