A wheel has a speed of 1200 revolution per minute and is made to slow down at a rate of 4 radian/s2. The number of revolutions it makes before coming to rest is
ω2=ω20−2αθ⇒0=4π2n2−2αθ
θ=(4π2120060)22×4=200π2 rad
∴2πn=200π2⇒n=100π=314 revolutions
Related Playlists
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -7 (GRAVITATION)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -7 (MECHANICAL PROPERTIES OF SOLIDS)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -5 (WORK, ENERGY AND POWER)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR30videos
ATOMS
- BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator30videos
COMMUNICATION SYSTEM
Similar Questions
A wheel has a speed of 1200 revolution per minute and is made to slow down at a rate of 4rad/s2. The number of revolutions it makes before coming to rest is
View SolutionThe wheel of a car makes 10rev/s. It is stopped in 14 s .Then the number of revolutions it makes before it stops
View SolutionA flywheel has moment of inertia 4kg−m2 and has kinetic energy of 200 J. Calculate the number of revolutions it makes before coming to rest if a constant opposing couple of 5N-m is applied to the flywheel
View SolutionThe angular speed of a fly wheel making 120 revolutions / minute is
View SolutionA flywheel is revolving at 150 revolutions per minutes .If deccelerates at a constant rate of 2πrad/s2, then time requred to stop it is
View SolutionThe angula speed of a fly-wheel making 120 revolutions /minute is :
View SolutionA table fan rotating at a speed of 2400 rpm is switched off and the resulating variation of the revolution/minute time is shown in Fig. The total number of revolutions of the fan before it comes to rest is
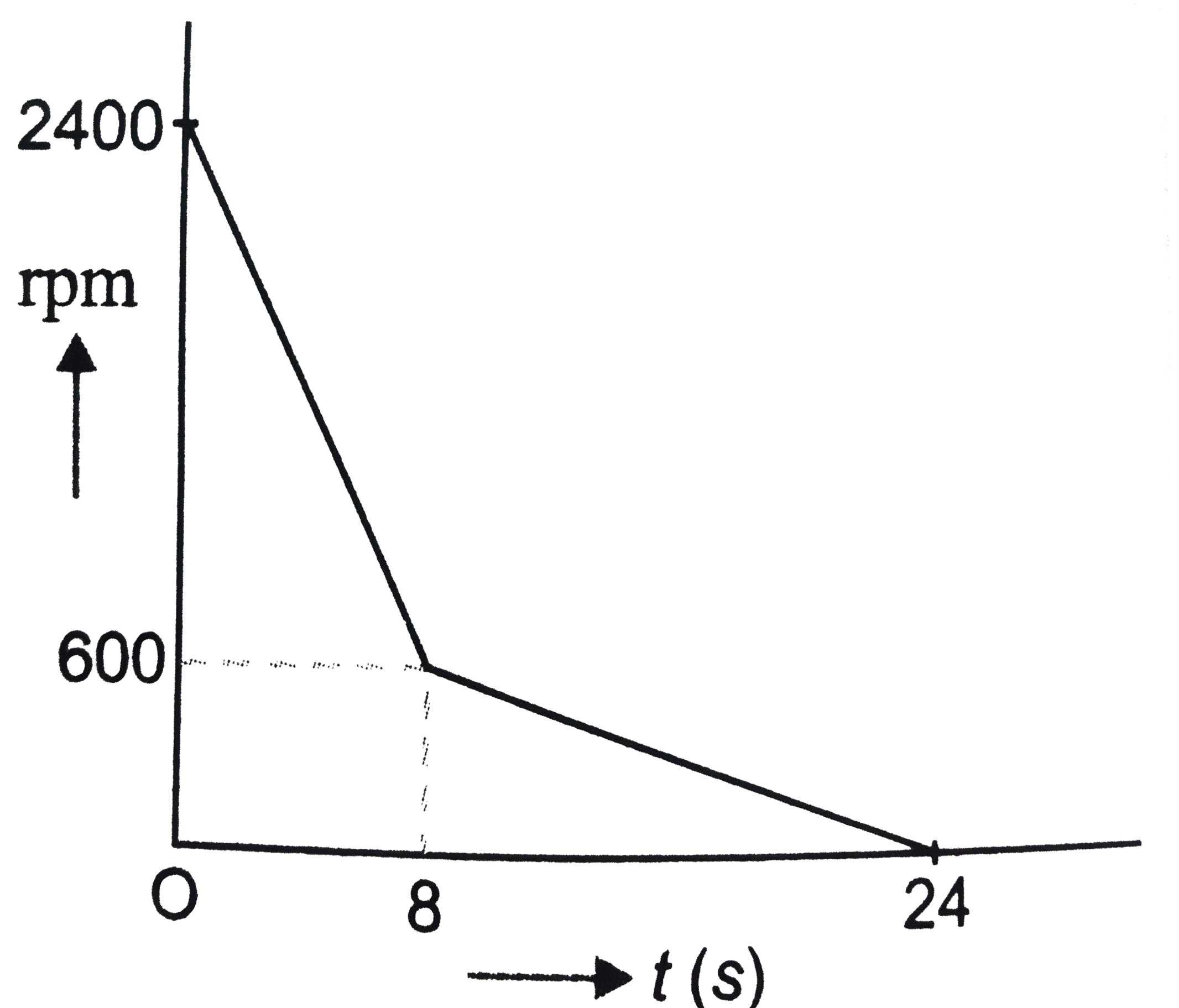 View Solution
View SolutionA wheel makes 360 revolutions per minute. Through how many radians does it turn in 1 second?
View SolutionA table fan rotating at a speed of 2400 revolutions per minute(rpm), is switched off and the resulting variation of the rpm with time is shown in the figure. Total number of revolutions of the fan before it comes to rest is
'(##CEN_KSR_PHY_JEE_C07_001_Q01##)'View SolutionThe angular velocity of a wheel increases from 120 to 480 rpm in 10 s .The number of revolutions made during this time is
View Solution


