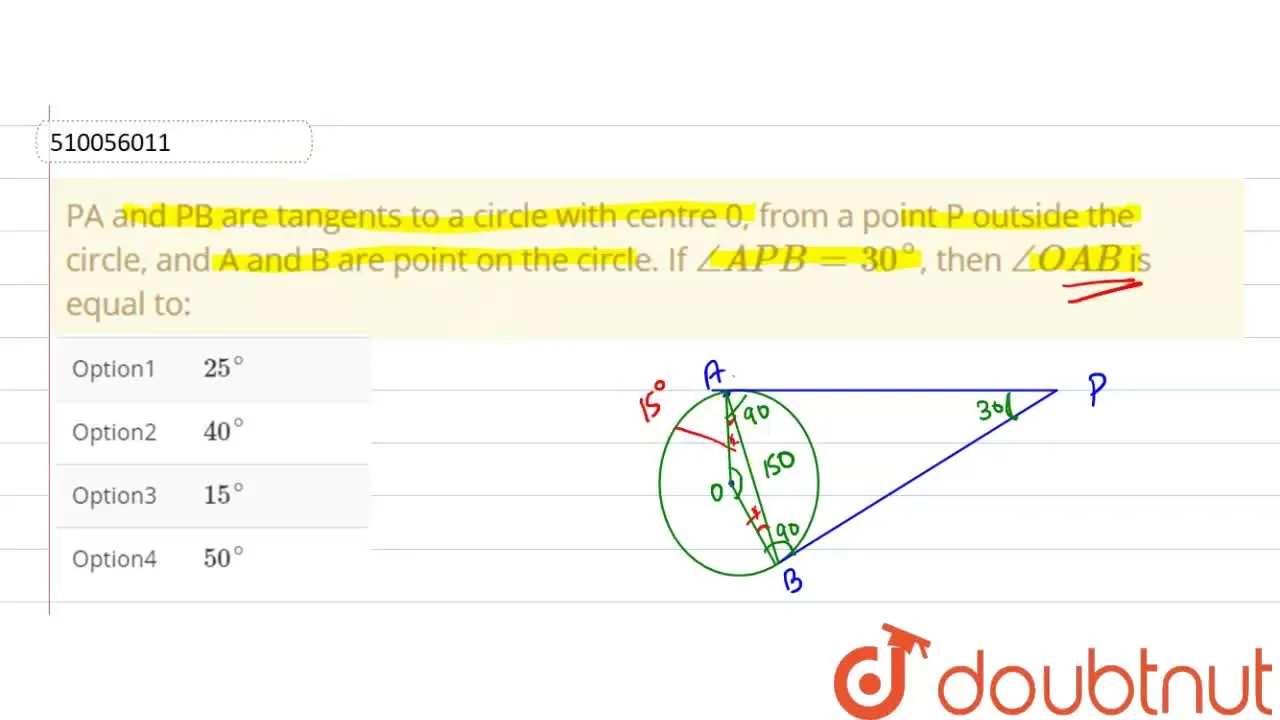
PA and PB are tangents to a circle with centre 0, from a point P outside the circle, and A and B are point on the circle. If ∠APB=30∘, then ∠OAB is equal to:
25∘
40∘
15∘
50∘
The correct Answer is:C
Step by step video, text & image solution for PA and PB are tangents to a circle with centre 0, from a point P outside the circle, and A and B are point on the circle. If angleAPB = 30^(@), then angleOAB is equal to: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
PA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If ∠APB=40∘, then ∠OAB is equal to:
PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=40∘ है, तो ∠OAB का मान ज्ञात करें |View SolutionPA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If ∠APB=70∘ then ∠OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠OAB=20∘, then ∠APB is equal to:
PA तथा PB केंद्र O वाले वृत के बाहर स्थित बिंदु P से वृत्त पर खींची गयी दो स्पर्श रेखाएं हैं | A और B वृत्त पर स्थित बिंदु हैं | यदि ∠OAB=20∘ है, तो ∠APB का मान कया होगा ?View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle A and B are points on the circle. If ∠APB=86∘, then ∠OAB is equal to:
PA तथा PB केंद्र O वाले वृत के बाहर स्थित बिंदु P से वृत्त पर खींची गयी दो स्पर्श रेखाएं हैं | A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=86∘ है, तो ∠OAB का ज्ञात करें |View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle A and B are points on the circle. If ∠OAB=38∘, then ∠APB is equal to:
PA तथा PB केंद्र O वाले वृत के बाहर स्थित बिंदु P से वृत्त पर खींची गयी दो स्पर्श रेखाएं हैं | A और B वृत्त पर स्थित बिंदु हैं | यदि ∠OAB=38∘, है, तो ∠APB का ज्ञात करें |View SolutionPA and PB are the tangents to a circle with centre O, from a point P outside the circle. A and B are the points on the circle. If ∠APB=72∘,then ∠OAB is equal to:
PA तथा PB एक वृत्त पर वृत्त के बाहर स्थित बिंदु P से खींची गयी स्पर्श रेखाएं हैं जिसका केंद्र O है | A तथा B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=72∘ है, तो ∠OAB का मान ज्ञात करें |View SolutionPA and PB are two tangents to a circle with centre O, from P outside the circle. A and B are points on the circle. If ∠APB=100∘, then ∠OAB is equal to :
केंद्र O वाले एक वृत्त के बाहर किसी बिंदु P से खींची गई दो स्पर्श रेखाएँ PA और PB हैं | वृत्त पर A और B बिंदु हैं | यदि ∠APB=100∘,तो ∠OAB का क्या होगा ?View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
View Solution