The x-coordiante of the incentre of the triangle that has the coordiantes of mid points of its sides as (0,1),(1,1) and (1,0) is:

A

2+√2

B

2−√2

C

1+√2

D

1−√2

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Given mid-points of a triangle are (0,1), (1,1) and (1,0). Plotting these points on a graph paper and make a triangle.
So, the sides of triangle will be 2,2 and √22+22 i.e. 2√2.
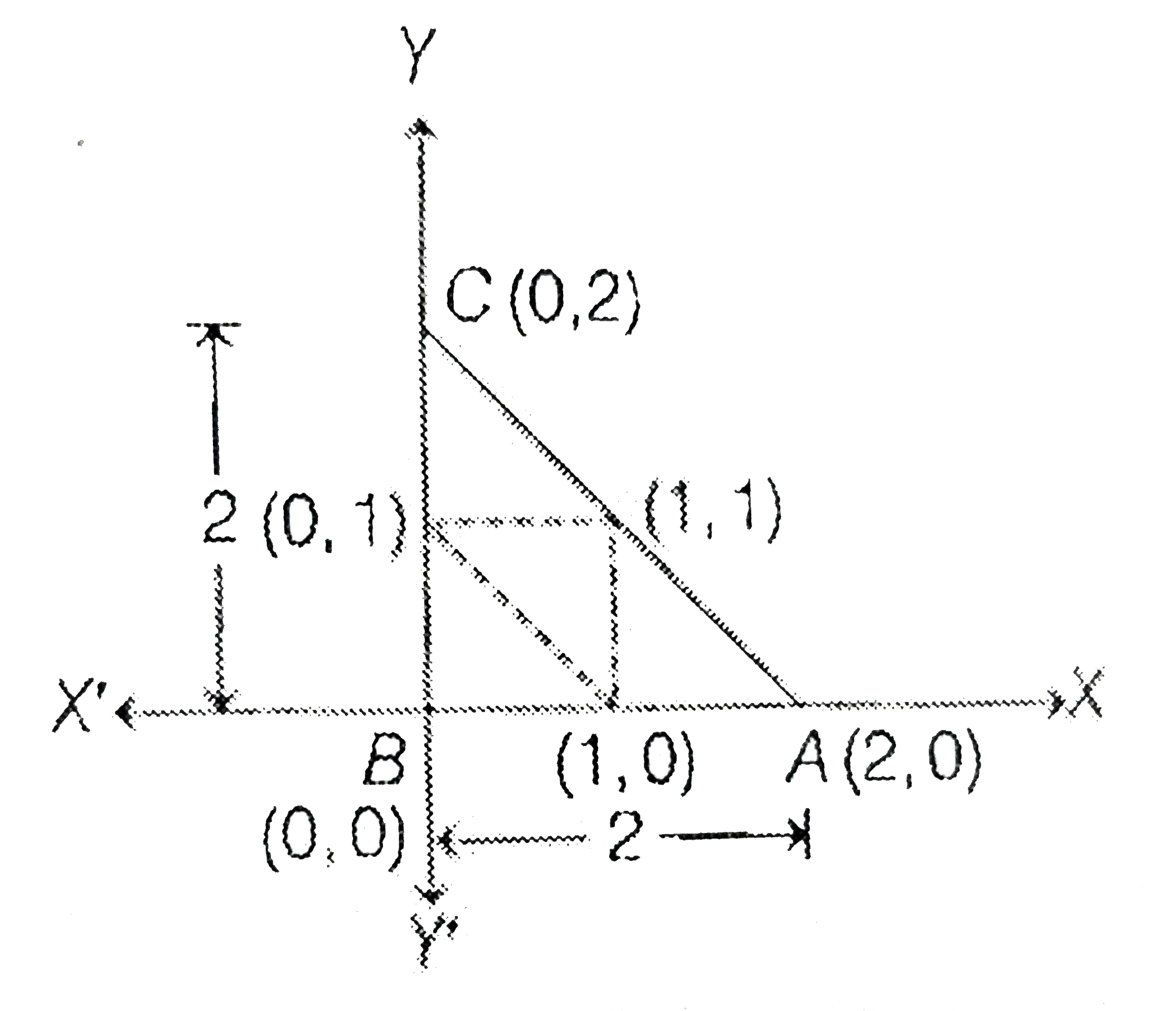
ocr_image
x-coordinate of incentre =2×0+2√2⋅0+2⋅22+2+2√2
=22+√2×2−√22−√2=2−√2

Updated on:21/07/2023
|
Class 12MATHSSTRAIGHT LINE AND PAIR OF STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The x -coordinate of the incentre of the triangle that has the coordinates of mid-points its sides are (0,1), (1,1) and (1, 0) is

    A2+√2
    B2−√2
    C1+√2
    D1−√2

  • The x -coordinate of the incentre of the triangle that has the coordinates of mid-points its sides are (0,1), (1,1) and (1, 0) is

    A2+√2
    B2−√2
    C1+√2
    D1−√2

  • The x-coordinates of the incentre of the triangle that has the coordinates of mid-point of its sides as (0, 1), (1, 1) and (1, 0), is

    A2+√2
    B2−√2
    C1+√2
    D1−√2