Let $k$ be an integer such that the triangle with vertices $(k, - 3 k), (5, k)$ and $(- k, 2)$ has area $28 s q \dot{}$ units. Then the orthocentre of this triangle is at the point :

A

$(2, - \frac{1}{2})$

B

$(1, \frac{3}{4})$

C

$(1, - \frac{3}{4})$

D

$(2, \frac{1}{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Given, vertices of triangle are $(k, - 3 k), (5, k)$ and $(- k, 2)$ .
$∴ \frac{1}{2} | \begin{matrix} k & - 3 k & 1 \\ 5 & k & 1 \\ - k & 2 & 1 \end{matrix} | = \pm 28$
$\Rightarrow | \begin{matrix} k & - 3 k & 1 \\ 5 & k & 1 \\ - k & 2 & 1 \end{matrix} | = \pm 56$
$\Rightarrow k (k - 2) + 3 k (5 + k) + 1 (10 + k^{2}) = \pm 56$
$\Rightarrow k^{2} - 2 k + 15 k + 3 k^{2} + 10 + k^{2} = \pm 56$
$\Rightarrow 5 k^{2} + 13 k + 10 = \pm 56$
$\Rightarrow 5 k^{2} + 13 k - 66 = 0$
or $5 k^{2} + 13 k - 46 = 0$
$\Rightarrow k = 2$ [ $∵ k \in I$ ]
Thus, the corrdinates of vertices of triangle are $A (2, - 6)$ , $B (5, 2)$ and $C (- 2, 2)$
Now, equation of altitude from vertex $A$ is
$y - (- 6) = \frac{- 1}{(\frac{2 - 2}{- 2 - 5})} (x - 2) \Rightarrow x = 2$ ....... $(i)$

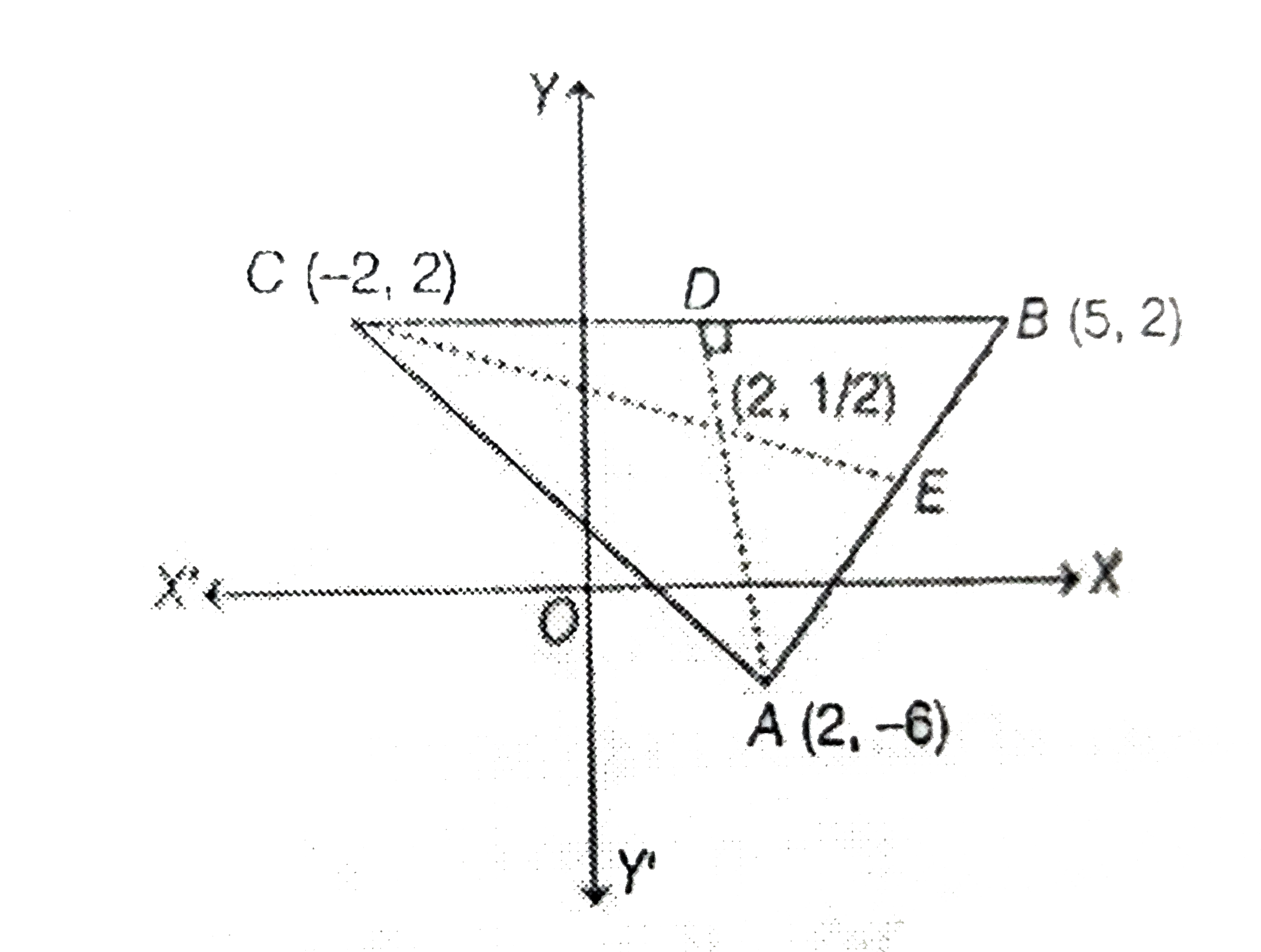
Equation of altitude from vertex $C$ is
$y - 2 = \frac{- 1}{[\frac{2 - (- 6)}{5 - 2}]} [x - (- 2)]$
$\Rightarrow 3 x + 8 y - 10 = 0$ ......... $(i i)$
On solving Eqs. $(i)$ and $(i i)$ , we get $x = 2$ and $y = \frac{1}{2}$ .
$∴$ Orthocentre $= (2, \frac{1}{2})$

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINE AND PAIR OF STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let k be an integer such that the triangle with vertices $(k, - 3 k), (5, k)$ and (-k, 2) has area 28 sq units. Then, the orthocentre of this triangle is at the point
A $(2, \frac{1}{2})$
B $(2, - \frac{1}{2})$
C $(1, \frac{3}{4})$
D $(1, - \frac{3}{4})$
If the area of triangle with vertices (-3,0), (3,0) and (0,k) is 9 sq . units then the value of k is
A9
B6
C3
D $- 9$
If the area of triangle with vertices (2,-6), (5,4) and (k,4) is 35. Then k equal to
A12 or 2
B12 or -2
C $- 12 or - 2$
D $- 12 or 2$

IIT JEE PREVIOUS YEAR-STRAIGHT LINE AND PAIR OF STRAIGHT LINES-GENERAL EQUATION OF PAIR OF STRAIGHT LINES (Objective Questions I) (Only one correct option)

Home
Ask Doubt
Profile