Let S be the set of all points in (−π,π) at which the Then, S is a subset of which of the following?
{−π4,0,π4}
{−π2,−π4,π4,π2}
{−3π4,−π4,3π4,π4}
{−3π4,−π2,π2,3π4}
The correct Answer is:C
Let us draw the graph of y = f(x), as shown below
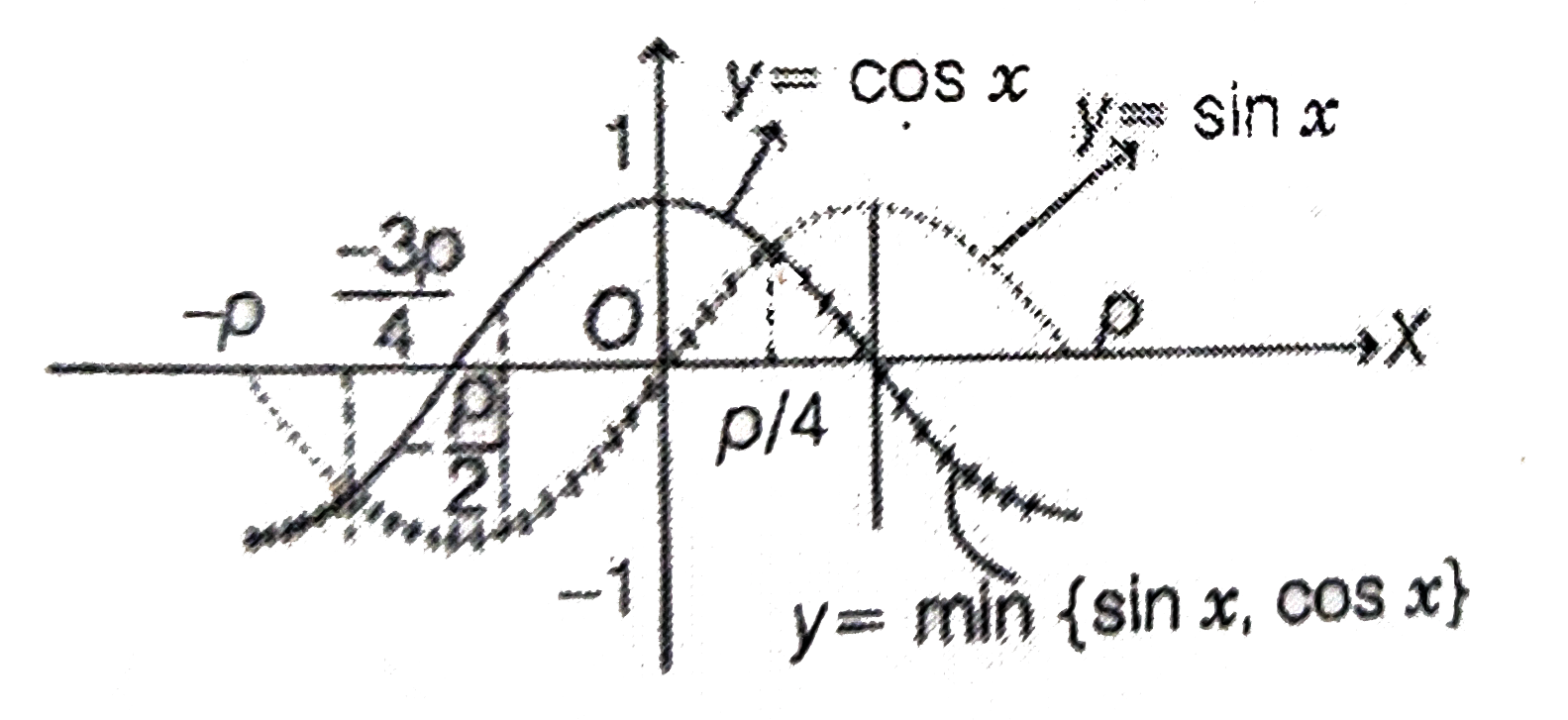
Clearly, the function f(x) = min { sin x, cos x}is not differentiable at x=−3π4andπ4 [these are point of intersection of graphs of sin x and cos x in (−π,π), on which function has sharp edges]. So, S={−3π4,π4}, which is a subset of {−3π4,−π4,3π4,π4}
Topper's Solved these Questions
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Differentiability at a point ( Objective Questions II)
Explore 15 Videos
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Differentiability at a point ( Assertion and Reason)
Explore 1 Video
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Continuity for Composition and Function (Analytical & Descriptive Questions)
Explore 4 Videos
- JEE MAINSBook:IIT JEE PREVIOUS YEARChapter:JEE MAINSExercise:All Questions
Explore 1 Video
- MATRICES AND DETERMINANTSBook:IIT JEE PREVIOUS YEARChapter:MATRICES AND DETERMINANTSExercise:SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
Explore 2 Videos
Similar Questions
Let S be the set of all sets and let R={(A,B):A⊂B},i.e., . A is a proper subset of B. Show that R is (i) Transitive (ii) Not reflexive (iii) not symmetric.
View SolutionLet S be the set of all points in a plane. Let R be a relation on S such that for any two points a and b, a R b iff b is within 1 centimetre from a. Check R for reflexivity, symmetry and transitivity.
View Solution
Knowledge Check
let S be the set of all points in (−π,π) at which the function , f(x) =min {sinx , cos x} is not differentiable Then S is a subset of which of the following ?
A{−3π4,−π4,3π4,π4}B1C2D3Let T be the line passing the points P(–2, 7) and Q(2,–5). Let F1 be the set of all pairs of circles (S1,S2) such that T is tangent to S1 at P and tangent to S2 at Q, and also such that S1 and S2 touch each other at a point, say M. Let E1 be the set representing the locus of M as the pair (S1,S2) varies in F1. Let the set of all straight line segments joining a pair of distinct points of E1 and passing through the point R(1,1,) be F2. Let E2 be the set of the mid-points of the line segments in the set F2. Then, which of the following statment(s) is (are) TRUE ?
AThe point (–2,7) lies in E1BThe point (45,75) does NOT lie in E2CThe point (12,1) lies in E2DThe point (0,32) does NOT lie in E1Let T be the line passing through the points P(-2, 7) and Q(2, -5). Let F1 be the set of all pairs of circles (S1,S2) such that T is tangent to S1 at P and tangent to S2 at Q, and also such that S1andS2 touch each other at a point , say M. Let E1 be the set representing the locus of M as the pair (S1,S2) varies in F1. Let the set of all straight line segment joining a pair of disntinct point of E1 and passing through the point R(1, 1) be F2. Let E2 be the set of the mid-points of the line segments in the set F2. Then , which of the following statement (s) is (are) TRUE?
AThe point (-2, 7) lies in E1BThe point (45,75) does NOT lie in E2CThe point (12,1) lies in E2DThe point (0,32)does NOT lie in E1
Let S be the set of all persons living in Delhi. We say that x, y in S are related if they were born in Delhi on the same day. Which one of the following is correct?
View SolutionConsider the set A of all determinants of order 3 with entries 0 or 1 only. Let B be the subset of A consisting of all determinants with value 1. Let C be the subset of the set of all determinants with value −1. Then
View SolutionLet S be the set of all possible values of parameter 'a' for which the points of intersection of the parabolas y2=3axandy=12(x2+ax+5) are concyclic. Then S contains the interval(s)
View SolutionIf V is a finite dimensional inner product space and S,S1andS2 are subset of V. then which of the following is not true?
View SolutionLet S be the set of all points with coordinates (x, y, z), where x,y and z are each chosen from the set [0, 1, 2). How many equilateral triangles have all their vertices in S?
View Solution

