Let f:(−1,1)→R be a function defind by f(x) =max. {−|x|,−√1−x2}. If K is the set of all points at which f is not differentiable, then K has set of all points at which f is not differentible, then K has exactly

A

three elements

B

five elements

C

two elements

D

one element

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Key Idea This type of questions can be solved graphically.
Given, f:(−1,1)→R, such that
f(x)=max {−|x|,−√1−x2}
On drawing the graph, we get the following figure.
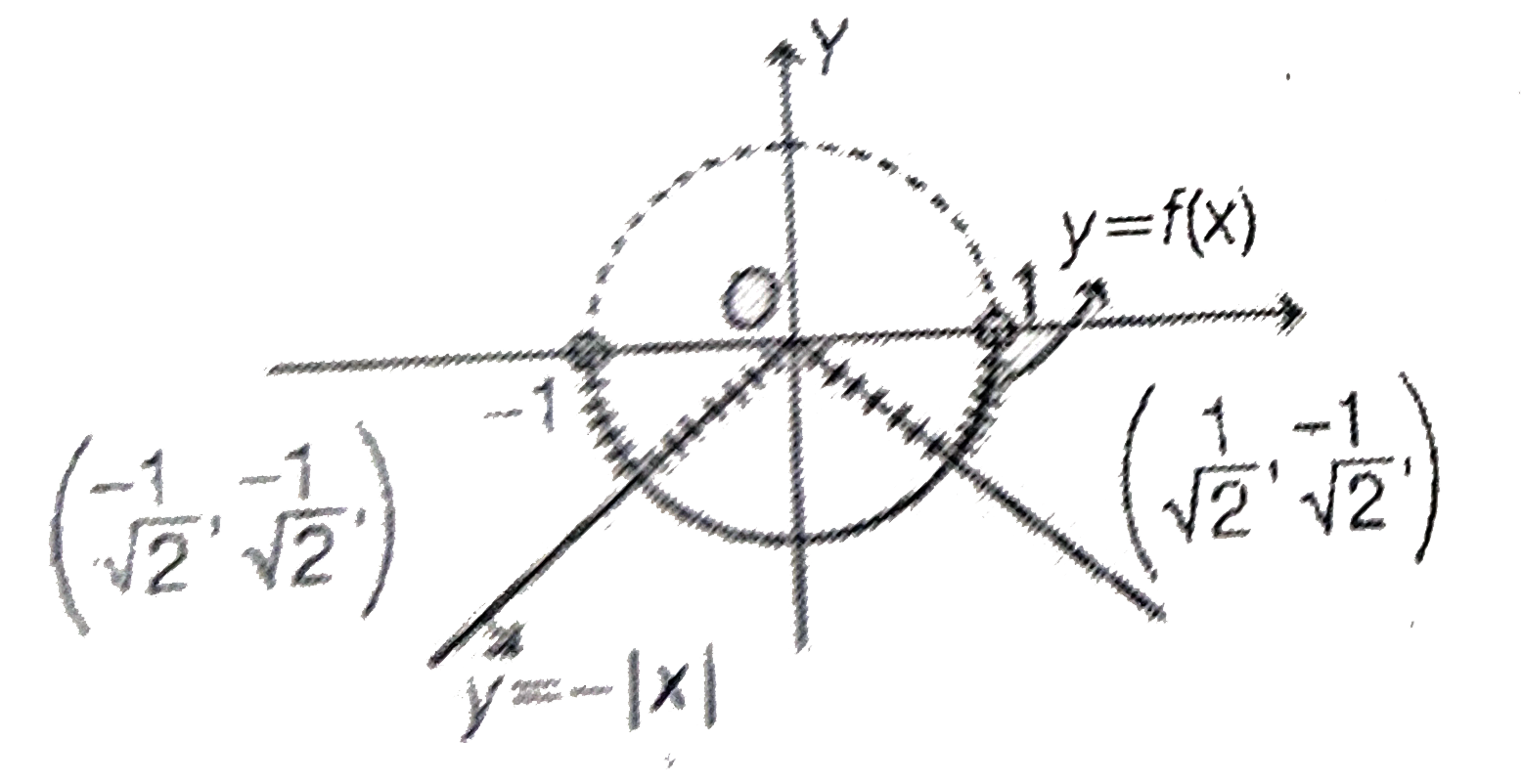
ocr_image
[∵graphpfy=−|x| is
ocr_image
and graph of y=−√1−x2
ocr_image
 [∵x2+y2=1 represent a complete circle]
⇒f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩−√1−x2, −1<x≤−1√2−|x|, −1√2<x≤1√2−√1−x2, 1√2<x<1
From the figure it is clear that function have sharp edges, at x=−1√2,0,1√2
∴ Function is not differentiable at 3 points.

Updated on:21/07/2023
|
Class 12MATHSLIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Let f:(−1,1)→R be a function defined by max {−|x|,−√1−x2}. If k be the set of all points at which f is not differentiable then k has exactly

    Athree elements
    Bone element
    Cfive elements
    Dtwo elements

  • Let f:R→R be a function defined by f(x)=max.{x,x3}. The set of all points where f(x) is NOT differenctiable is
    (a) {−1,1}
    (b) {−1,0}
    (c ) {0,1}
    (d) {−1,0,1}

    A{−1,1}
    B{−1,0}
    C{0,1}
    D{−1,0,1}

  • Let f:[−1,1]→R be a function defined by f(x)={x2∣∣cos(πx)∣∣forx≠0,for x=0, The set of points where f is not differentiable is

    A{x∈[−1,1],x≠0}
    B[x∈0−1,1]:x=0 or x=22n+1,n∈Z}
    C{x∈[−1,1]:x=22n+1,n∈Z}
    D[−1,1]