An object moves in such a way that its position (in meters) as a function of time (in seconds) is →r=ˆi+3t2ˆj+tˆk. Give expressions for (a) the velocity of the object and (b) the acceleration of the object as functions of time.
To solve the problem, we need to find the expressions for the velocity and acceleration of the object given its position vector as a function of time.
Given:
The position vector of the object is given by:
→r=^i+3t2^j+t^k
(a) Finding the Velocity of the Object
The velocity vector →v is defined as the rate of change of the position vector with respect to time. Mathematically, this is expressed as:
→v=d→rdt
Step 1: Differentiate the Position Vector
We differentiate each component of the position vector →r:
- The x-component (coefficient of ^i) is 1, which differentiates to 0.
- The y-component (coefficient of ^j) is 3t2, which differentiates to 6t (using the power rule).
- The z-component (coefficient of ^k) is t, which differentiates to 1.
Thus, the velocity vector is:
→v=0^i+6t^j+1^k
or simply:
→v=6t^j+^k
(b) Finding the Acceleration of the Object
The acceleration vector →a is defined as the rate of change of the velocity vector with respect to time. Mathematically, this is expressed as:
→a=d→vdt
Step 2: Differentiate the Velocity Vector
We differentiate each component of the velocity vector →v:
- The x-component (coefficient of ^i) is 0, which differentiates to 0.
- The y-component (coefficient of ^j) is 6t, which differentiates to 6.
- The z-component (coefficient of ^k) is 1, which differentiates to 0.
Thus, the acceleration vector is:
→a=0^i+6^j+0^k
or simply:
→a=6^j
Final Expressions
- Velocity: →v=6t^j+^k
- Acceleration: →a=6^j
The position vector of the object is given by:
→r=^i+3t2^j+t^k
→v=d→rdt
We differentiate each component of the position vector →r:
- The x-component (coefficient of ^i) is 1, which differentiates to 0.
- The y-component (coefficient of ^j) is 3t2, which differentiates to 6t (using the power rule).
- The z-component (coefficient of ^k) is t, which differentiates to 1.
→v=0^i+6t^j+1^k
or simply:
→v=6t^j+^k
→a=d→vdt
We differentiate each component of the velocity vector →v:
- The x-component (coefficient of ^i) is 0, which differentiates to 0.
- The y-component (coefficient of ^j) is 6t, which differentiates to 6.
- The z-component (coefficient of ^k) is 1, which differentiates to 0.
→a=0^i+6^j+0^k
or simply:
→a=6^j
- Velocity: →v=6t^j+^k
- Acceleration: →a=6^j
Topper's Solved these Questions
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
49 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
3 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT
3 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
Similar Questions
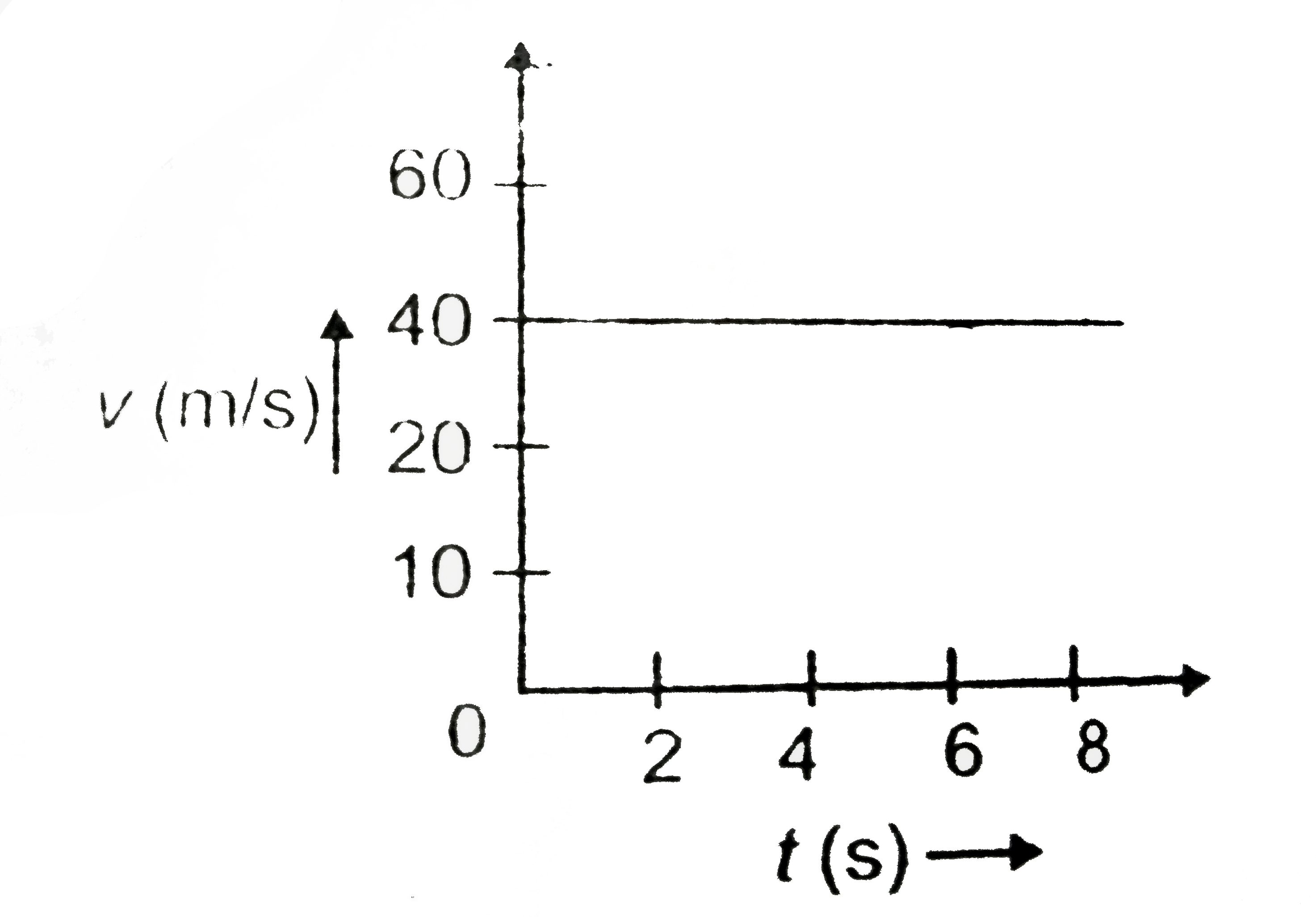
The velocity-time graph of an object is shown below. The acceleration of the object is
View SolutionA particle moves in such a way that its position vector at any time tist "is" hati+12t2ˆj+tˆK Find a function of time (a) the velocity, (b) the speed, (c) the acceleration, (d) the magnitude of the acceleration, (e) the magnitude of the component of acceleration along velocity (called tangential' acceleration), (f) the magnitude of the component ofacceleration perpendicular to velocity (called normal acceleration).
View Solution
Knowledge Check
A point moves such that its displacement as a function of times is given by x2=t2+1. Its acceleration at time t is
A1x3B−1x2C1x−t2x3D1x−tx3An object is moving in the x-y plane with the position as a function of time given by →r=x(t)ˆi+y(t)ˆj. Point O is at x=0,y=0 . The object is definitely moving towards O when
Avx>0,vy>0Bvx<0,vy<0Cxvx+yvy<0Dxvx+yvy>0
The position of a particel is expressed as →r=(4t2ˆi+2tˆj) m. where t is time in second. Find the acceleration of the particle.
View SolutionThe position of a particle is given by →r=(8tˆi+3t2ˆj+5ˆk)m where t is measured in second and →r in meter. Calculate, the velocity and the acceleration of the particle.
View SolutionThe displacement x of an object is given as a function of time x=2t+3t2
Calculate the instantaneous velocity of the object at t = 2 s
View SolutionA force acts on a 2 kg object so that its position is given as a function of time as x=3t2+5. What is the work done by this force in first 5 seconds ?
View SolutionA car is moving in such a ways that the distance it covers , is given by the equations s=4t2+3t, where s, is in meters and t is in seconds . What would be the velocity and the accelerations of the car at time t=20 seconds?
View SolutionA particle moves in xy plane with its position vector changing with time (t) as →r=(sint)ˆi+(cost)ˆj ( in meter)
Find the tangential acceleration of the particle as a function of time. Describe the path of the particle.
View Solution