There is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as D where particle finally strikes. Acceleration due to gravity
How much time the particle takes to cross the point C after being projected from point A.
1s
2s
3s
4s
The correct Answer is:d
To solve the problem step by step, we will analyze the motion of the particle projected from the top of the tower.
Step 1: Understand the motion of the particle
The particle is projected upwards from point A (top of the tower) with an initial speed of u=20m/s. The height of the tower is h=20m. The acceleration due to gravity is g=10m/s2, acting downwards.
Step 2: Determine the time taken to reach the maximum height (point B)
At the maximum height, the final velocity v=0. We can use the first equation of motion:
v=u−gt
Substituting the known values:
0=20−10t
Solving for t:
10t=20⟹t=2s
Thus, the time taken to reach point B from point A is 2s.
Step 3: Determine the time taken to return to point A (point C)
Since the motion from A to B and from B to C is symmetric, the time taken to return from B to C is also 2s.
Step 4: Calculate the total time to cross point C
The total time taken to cross point C (which includes the time to go up to B and come back down to C) is:
Total time=Time from A to B+Time from B to C=2s+2s=4s
Final Answer
The particle takes 4 seconds to cross point C after being projected from point A.
---
The particle is projected upwards from point A (top of the tower) with an initial speed of u=20m/s. The height of the tower is h=20m. The acceleration due to gravity is g=10m/s2, acting downwards.
At the maximum height, the final velocity v=0. We can use the first equation of motion:
v=u−gt
Substituting the known values:
0=20−10t
Solving for t:
10t=20⟹t=2s
Thus, the time taken to reach point B from point A is 2s.
Since the motion from A to B and from B to C is symmetric, the time taken to return from B to C is also 2s.
The total time taken to cross point C (which includes the time to go up to B and come back down to C) is:
Total time=Time from A to B+Time from B to C=2s+2s=4s
The particle takes 4 seconds to cross point C after being projected from point A.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (ASSERTION REASON)
9 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (MATCHING TYPE QUESTIONS)
2 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( C.(MULTIPLE CHOICE QUESTIONS))
13 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
There is one tower of height h. one particle A is projected upward from top of the tower with a speed u1 at time t=0 . At time t=t0 another particle B is projected upward from the bottom of the tower with a speed u2. When will the particles cross each other?
View SolutionA particle is dropped from the top of a tower. It covers 40 m in last 2s. Find the height of the tower.
View Solution
Knowledge Check
There is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as D where particle finally strikes. Acceleration due to gravity g=10m/s2
Time taken by the particle to reach the ground isA2sB4sC2√2sD(2+2√2)sThere is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as Dwhere particle finally strikes. Acceleration due to gravity g=10m/s2
Maximum height above the ground attained by particle isA20mB30mC40mD60mAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
A20√3mB20√3mC√320mDNone of these
Height of a tower is 125m and a particle is dropped from rest from the top of the tower. After two seconds of its fall, another particle is projected downwards with a speed u such that both the particles reach the ground simultaneously. What is the value of u?
View SolutionA particle is dropped from the top of a tower. If it falls half of the height of the tower in its last second of journey, find the time of journey.
View SolutionA particle is dropped from the top of a tower. During its motion it covers 925 part of height of tower in the last 1 second Then find the height of tower.
View SolutionA particle is thrown horizontally from a tower of height 20m. If the speed of projection is 20ms then the distance of point from the tower,where the particle hit the ground is:-
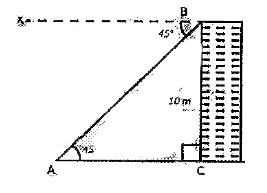
View SolutionSuppose angle of depression from top of the tower to point A is 45∘ and height of tower is 10 m. What is the distance of point A from the building?
View Solution
