There is one tower of height h. one particle A is projected upward from top of the tower with a speed u1 at time t=0 . At time t=t0 another particle B is projected upward from the bottom of the tower with a speed u2. When will the particles cross each other?
To solve the problem of when two particles A and B cross each other, we can follow these steps:
Step 1: Understand the motion of both particles
- Particle A is projected upwards from the top of a tower of height h with an initial speed u1 at time t=0.
- Particle B is projected upwards from the ground with an initial speed u2 at time t=t0.
Step 2: Determine the equations of motion for both particles
- For Particle A (projected at t=0):
- The height yA of Particle A at time t is given by:
yA=h+u1t−12gt2
- For Particle B (projected at t=t0):
- The height yB of Particle B at time t (where t is the total time since A was projected) is given by:
yB=u2(t−t0)−12g(t−t0)2
- This equation is valid for t≥t0.
Step 3: Set the heights equal to find the crossing point
- The particles cross each other when their heights are equal:
yA=yB
Substituting the equations from above:
h+u1t−12gt2=u2(t−t0)−12g(t−t0)2
Step 4: Simplify the equation
- Rearranging the equation gives:
h+u1t−12gt2=u2t−u2t0−12g(t2−2tt0+t20)
- Expanding and simplifying:
h+u1t−12gt2=u2t−u2t0−12gt2+gt0t−12gt20
- Canceling −12gt2 from both sides:
h+u1t=u2t−u2t0+gt0t−12gt20
Step 5: Rearranging to isolate terms
- Rearranging gives:
h+u1t+u2t0−12gt20=(u2+gt0)t
- Thus:
t=h+u1t+u2t0−12gt20u2+gt0
Step 6: Solve for t
- This equation can be solved for t to find the time at which the two particles cross each other.
- Particle A is projected upwards from the top of a tower of height h with an initial speed u1 at time t=0.
- Particle B is projected upwards from the ground with an initial speed u2 at time t=t0.
- For Particle A (projected at t=0):
- The height yA of Particle A at time t is given by:
yA=h+u1t−12gt2
- For Particle B (projected at t=t0):
- The height yB of Particle B at time t (where t is the total time since A was projected) is given by:
yB=u2(t−t0)−12g(t−t0)2
- This equation is valid for t≥t0.
- The particles cross each other when their heights are equal:
yA=yB
Substituting the equations from above:
h+u1t−12gt2=u2(t−t0)−12g(t−t0)2
- Rearranging the equation gives:
h+u1t−12gt2=u2t−u2t0−12g(t2−2tt0+t20)
- Expanding and simplifying:
h+u1t−12gt2=u2t−u2t0−12gt2+gt0t−12gt20
- Canceling −12gt2 from both sides:
h+u1t=u2t−u2t0+gt0t−12gt20
- Rearranging gives:
h+u1t+u2t0−12gt20=(u2+gt0)t
- Thus:
t=h+u1t+u2t0−12gt20u2+gt0
- This equation can be solved for t to find the time at which the two particles cross each other.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - NCERT (TEXTBOOK EXERCISES )
22 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - NCERT (ADDITIONAL EXERCISE)
6 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CONCEPTUAL QUESTIONS
14 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
A particle is projected up with initial speed u=10ms−1 from the top of a building at time t=0. At time t=5s the particle strikes the ground. Find the height of the building in meter.
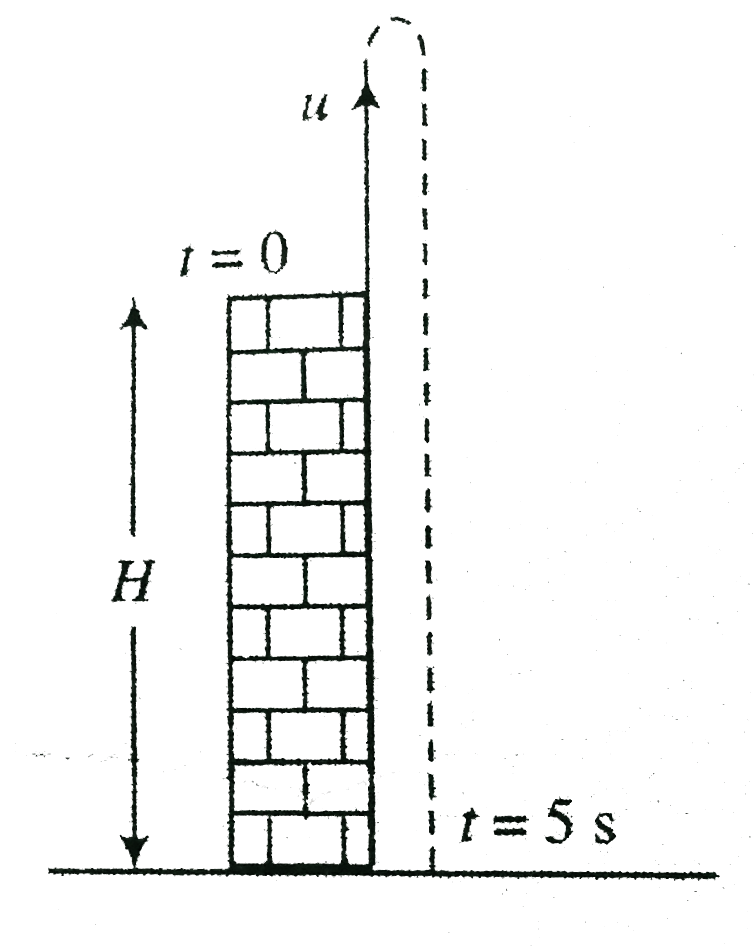 .
.
View SolutionHeight of a tower is 125m and a particle is dropped from rest from the top of the tower. After two seconds of its fall, another particle is projected downwards with a speed u such that both the particles reach the ground simultaneously. What is the value of u?
View Solution
Knowledge Check
A particle is projected vertically upwards in vacuum with a speed u.
AWhen it rises to half its maximum height, its speed becomes u/2.BWhen it rises to half its maximum height, its speed becomes u/√2.CThe time taken to rise to half its maximum height is half the time taken to reach its maximum height.DThe time taken to rise to three− fourth of its maximum height is half the time taken to reach its maximum height.There is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as D where particle finally strikes. Acceleration due to gravity g=10m/s2
Time taken by the particle to reach the ground isA2sB4sC2√2sD(2+2√2)sThere is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as Dwhere particle finally strikes. Acceleration due to gravity g=10m/s2
Maximum height above the ground attained by particle isA20mB30mC40mD60m
A ball is prouected vertical up from the top of a cliff of height h with a speed v1 Another ball is projected vertically up with a speed v2 from the bottom of the cliff, after a time t0 from the instantof projection of the first ball, When will the balls meet?.
View SolutionThere is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as D where particle finally strikes. Acceleration due to gravity g=10m/s2
How much time the particle takes to cross the point C after being projected from point A.
View SolutionA particle is dropped from rest from the top of a building of height 100m. At the same instant another particle is projected upward from the bottom of the building What should be the speed of projection of the particle projected from the bottom of building so that the particle cross each other after 1s? Acceleration due to gravity is 10 m/s2.
View SolutionA ball is dropped from top of a tower of 100 m height. Simultaneously another ball was thrown upward from bottom of the tower with a speed of 50m/s(g=10m/s2). They will cross each other after
View SolutionA stone is dropped from the top of a 400m high tower. At the same time another stone is projected vertically upwards from the ground with a speed of 50m/s. The two stones will cross each other after a time
View Solution
