A particle is moving on a straight line and its average velocity is found to be zero in an interval of time.
Average speed of the particle may also be zero for a given interval of time.
Velocity of the particle can never be zero in given interval of time.
Velocity of the particle must be zero at a particular instant.
Acceleration of particle may be zero.
The correct Answer is:c
To solve the problem of a particle moving on a straight line with an average velocity of zero over a given interval of time, we can break down the solution into several steps:
1. Understanding Average Velocity:
The average velocity (vavg) of a particle is defined as the total displacement (Δx) divided by the total time taken (Δt):
vavg=ΔxΔt
2. Given Condition:
We are given that the average velocity is zero over a certain interval of time. This implies:
vavg=0⟹Δx=0
Therefore, the total displacement of the particle during this time interval is zero.
3. Interpreting Displacement:
If the displacement is zero, it means that the final position of the particle (X2) is equal to its initial position (X1):
X2−X1=0⟹X2=X1
This indicates that the particle has returned to its starting point after the time interval.
4. Velocity at a Particular Instant:
Since the particle has returned to its original position, it is possible that at some point during its motion, the particle must have come to a stop (velocity = 0) before changing direction to return to the starting point. This is a critical observation.
5. Acceleration Consideration:
For the particle to return to its starting position, it must have experienced some form of acceleration, which could be acting in the opposite direction to its motion. This means that the particle's speed would decrease to zero at some instant before it changes direction.
6. Conclusion:
Thus, we can conclude that:
- The average velocity is zero because the displacement is zero.
- The velocity of the particle must be zero at some instant during the motion for it to return to its starting position.
Final Answer:
The correct option is that the velocity of the particle must be zero at a particular instant.
---
The average velocity (vavg) of a particle is defined as the total displacement (Δx) divided by the total time taken (Δt):
vavg=ΔxΔt
We are given that the average velocity is zero over a certain interval of time. This implies:
vavg=0⟹Δx=0
Therefore, the total displacement of the particle during this time interval is zero.
If the displacement is zero, it means that the final position of the particle (X2) is equal to its initial position (X1):
X2−X1=0⟹X2=X1
This indicates that the particle has returned to its starting point after the time interval.
Since the particle has returned to its original position, it is possible that at some point during its motion, the particle must have come to a stop (velocity = 0) before changing direction to return to the starting point. This is a critical observation.
For the particle to return to its starting position, it must have experienced some form of acceleration, which could be acting in the opposite direction to its motion. This means that the particle's speed would decrease to zero at some instant before it changes direction.
Thus, we can conclude that:
- The average velocity is zero because the displacement is zero.
- The velocity of the particle must be zero at some instant during the motion for it to return to its starting position.
The correct option is that the velocity of the particle must be zero at a particular instant.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:COMPETITION FILE ( D.(MULTIPLE CHOICE QUESTIONS))
Explore 9 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:COMPETITION FILE (ASSERTION REASON)
Explore 9 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS))
Explore 74 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
Similar Questions
A material particle is moving along a straight line in such a manner that its velocity varies as shown in the figure. At which moment in time numbered successively on the time axis will the acceleration of the particle be maximal? How should one use the graph to determine the average velocity of motion over the time interval from t1 to t2 ?
View SolutionThe diagram shows the displacement-time graph for the particle moving in a straight line. What is average speed (in m/s) for the interval 0-10 s?

View Solution
Knowledge Check
The diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.
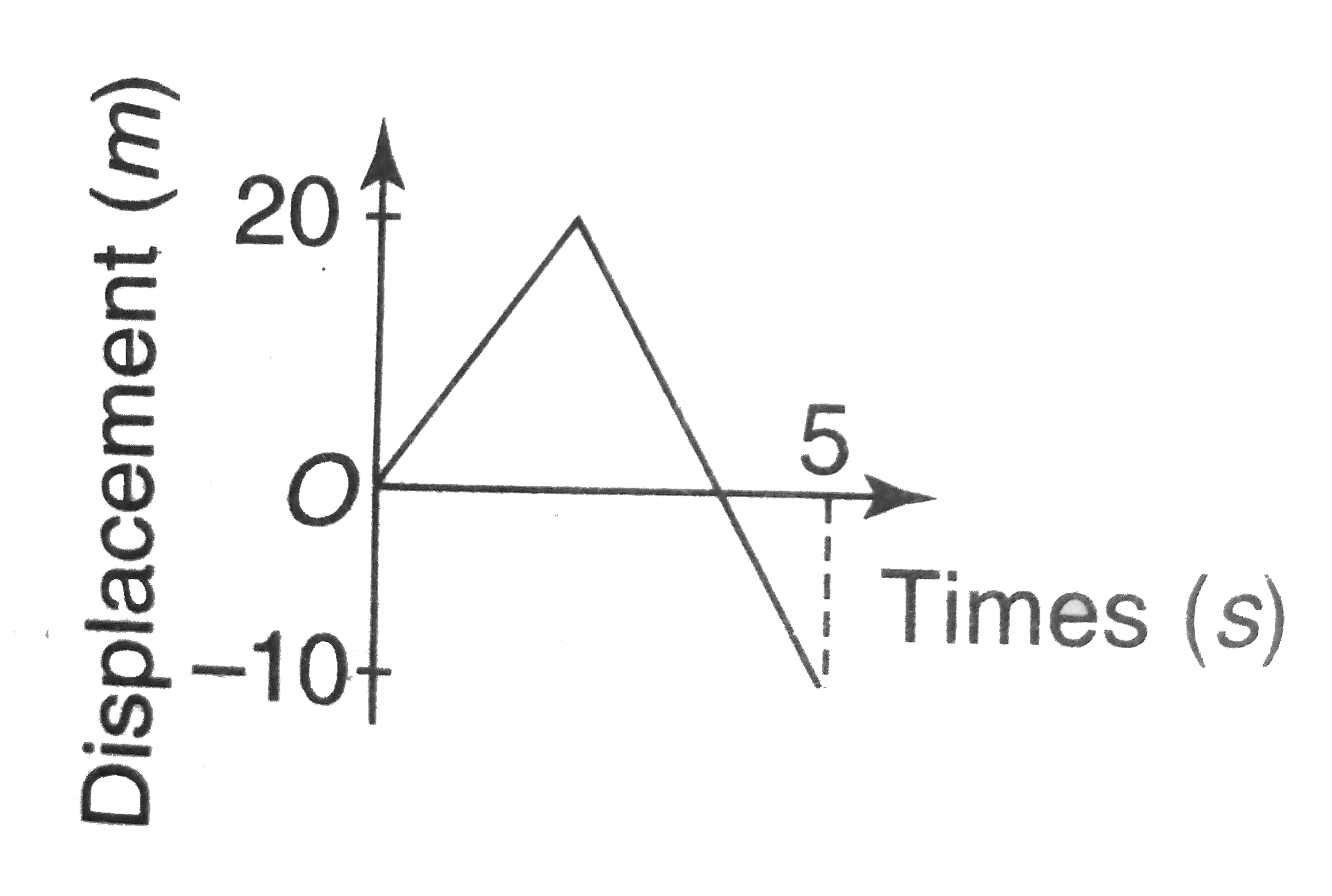 A−2ms−1B2ms−1C−4ms−1D4ms−1
A−2ms−1B2ms−1C−4ms−1D4ms−1The diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.
 A−2ms−1B2ms−1C−4ms−1D4ms−1
A−2ms−1B2ms−1C−4ms−1D4ms−1A particle is moving in a straight line with uniform velocity. Its acceleration is
ApositiveBnegativeCzeroDnone of these
A particle is moving in a straight line with uniform velocity. Its acceleration is
View SolutionMagnitude of average velocity and speed are found to be the saame in an interval of time.
View SolutionSTATEMENT-1: When a particle move along a straight line magnitude of its average velocity is equal to its average speed over any time interval provided particle does not return to path.
STATEMENT-2: For one dimensional motion displacement and distance both are same.
View SolutionA particle is moving on a straight line such that square of its velocity is directly proportional to distance as shown in graph. What is the acceleration of the particle ?
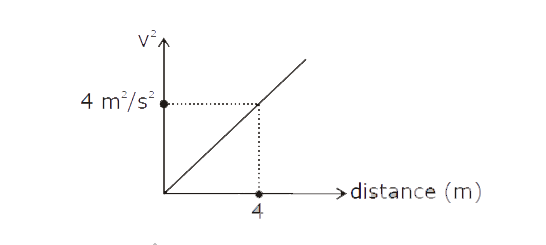
View SolutionStatement-I : A particle moves in a straight line with constant acceleration. The average velocity of this particle cannot be zero in any time interval.
Statement-II : For a particle moving in straight line with constant acceleration, the average velocity in a time interval is u+v2, where u and v are initial and final velocity of the particle of the given time interval.
View Solution