The radius ratio of an ionic solid r+/r− is 0.524. The coordination number of this type of structure is
The correct Answer is:6
To determine the coordination number of an ionic solid given the radius ratio r+/r−=0.524, we can follow these steps:
Step 1: Understand the Radius Ratio
The radius ratio r+/r− is the ratio of the radius of the cation (r+) to the radius of the anion (r−). This ratio helps us determine the coordination number of the ionic solid.
Step 2: Identify the Coordination Number Ranges
We need to refer to the established ranges for the radius ratio and their corresponding coordination numbers:
- If r+/r−<0.155, then coordination number = 2
- If 0.155<r+/r−<0.225, then coordination number = 3
- If 0.225<r+/r−<0.414, then coordination number = 4
- If 0.414<r+/r−<0.732, then coordination number = 6
- If 0.732<r+/r−<1, then coordination number = 8
Step 3: Compare the Given Radius Ratio
Now, we compare the given radius ratio 0.524 with the ranges we identified:
- Since 0.414<0.524<0.732, this indicates that the coordination number is 6.
Step 4: Conclusion
Thus, the coordination number of the ionic solid with a radius ratio of 0.524 is 6.
Summary of Steps:
1. Understand the radius ratio and its significance.
2. Identify the ranges for coordination numbers based on the radius ratio.
3. Compare the given radius ratio with the established ranges.
4. Conclude the coordination number based on the comparison.
The radius ratio r+/r− is the ratio of the radius of the cation (r+) to the radius of the anion (r−). This ratio helps us determine the coordination number of the ionic solid.
We need to refer to the established ranges for the radius ratio and their corresponding coordination numbers:
- If r+/r−<0.155, then coordination number = 2
- If 0.155<r+/r−<0.225, then coordination number = 3
- If 0.225<r+/r−<0.414, then coordination number = 4
- If 0.414<r+/r−<0.732, then coordination number = 6
- If 0.732<r+/r−<1, then coordination number = 8
Now, we compare the given radius ratio 0.524 with the ranges we identified:
- Since 0.414<0.524<0.732, this indicates that the coordination number is 6.
Thus, the coordination number of the ionic solid with a radius ratio of 0.524 is 6.
1. Understand the radius ratio and its significance.
2. Identify the ranges for coordination numbers based on the radius ratio.
3. Compare the given radius ratio with the established ranges.
4. Conclude the coordination number based on the comparison.
Topper's Solved these Questions
- SOLID STATEBook:MODERN PUBLICATIONChapter:SOLID STATEExercise:UNIT PRACTICE TEST
Explore 13 Videos
- SOLID STATEBook:MODERN PUBLICATIONChapter:SOLID STATEExercise:COMPETITION FILE - OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS)
Explore 3 Videos
- POLYMERSBook:MODERN PUBLICATIONChapter:POLYMERSExercise:Competition file (OBJECTIVE TYPE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS)(Integer Type Questions)
Explore 6 Videos
- SOLUTIONSBook:MODERN PUBLICATIONChapter:SOLUTIONSExercise:UNIT PRACTICE TEST
Explore 14 Videos
Similar Questions
Knowledge Check
An ionic crystal has rc/ra radius of 0.542. Its coordination number is
A2B6C4D8For coordination number-4, the limiting radius ratio is
A0.414B0.732C0.225D0.155An ionic crystal lattice has r+/r− radius ratio of 0.524, its coordination number is
A2B4C6D8
For an ionic solid of the genral formula AB and coordination number 6 , the value of the radius ratio will be
View SolutionRadius ratio of an ionic compound is 0.93. The structure of the above ionic compound is of
View SolutionFor a solid with the following structure, the coordination number of the point B is
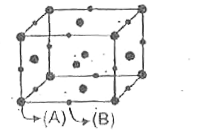
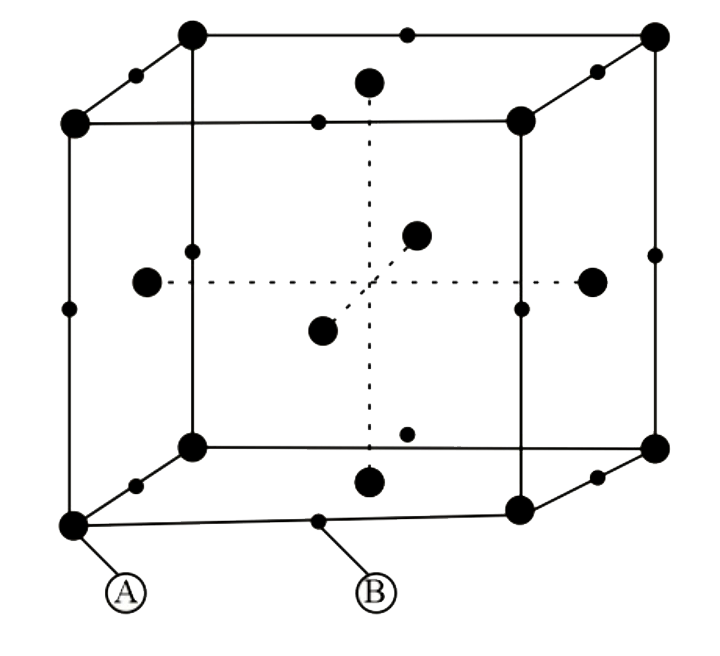
View SolutionFor a solid with the following structure, the coordination number of the point B is
View SolutionIn the crystalline solids the smallest repeating part in the lattice is known as unit cell. The unit cells are described as simple (points at all corners), body centred (points at all the corners and it the centre), face centred (points at all the corners and centre of all faces), and end centred (points at all hte corners and centres of two opposite and faces) unit cells. In two common tyupes of packing ccp and hcp, 26% of space is left unoccupied in the form of interstitial sites. For the stable ionic crystalline structures, there is difinite radius ratio limit for a cation to fit perfectly in the lattice of anions, called radius ratio rule. This also defines the coordination number of an ion, which is the number of nearest neighbours of opposite charges. This depeds upon the ratio of radii of two types of ions, r+/r−. This ratio for coordination numbers 3,4,6,and 8 is respectively 0.155 - 0.225, 0.225 - 0.414, 0.414 - 0.732 and 0.732 - 1 respectively.
The ionic radii of K+,Rb+andBr− are 137, 148 and 195 pm. The coordination number of cation in RbBr and KBr structures are respectively
View Solution

