The crate in Fig. 11-20 has dimensions I by h and the ramp is inclined at θ to the horizontal. Find the maximum θ for which it does not topple. Coefficient of friction between ramp and crate is μ.
To solve the problem of finding the maximum angle θ for which the crate does not topple on the inclined ramp, we will follow these steps:
Step 1: Understand the Forces Acting on the Crate
The crate experiences several forces:
- The gravitational force Mg acting downwards at its center of mass.
- The normal force R2 acting perpendicular to the surface of the ramp.
- The frictional force F acting parallel to the surface of the ramp.
Step 2: Identify the Conditions for Toppling
The crate will begin to topple when the normal force R1 at the edge of the ramp becomes zero. At this point, the torque due to the weight of the crate about the edge of the ramp will be balanced by the torque due to friction.
Step 3: Draw the Free Body Diagram (FBD)
In the FBD, we can break down the weight of the crate into two components:
- The component parallel to the ramp: Mgsinθ
- The component perpendicular to the ramp: Mgcosθ
Step 4: Set Up the Torque Equation
Taking torques about the edge of the ramp (where R1=0):
- The torque due to R2 (which is acting upwards) is R2⋅L2.
- The torque due to the weight of the crate (acting downwards) is Mgcosθ⋅L2.
Setting the torques equal for equilibrium:
R2⋅L2=Mgcosθ⋅L2
Step 5: Relate Friction to Normal Force
The frictional force can be expressed as:
F=μR2
Since F must balance the component of the weight acting down the ramp:
Mgsinθ=μR2
Step 6: Substitute R2 in Terms of θ
From the torque equation, we can express R2:
R2=Mgcosθ
Substituting this into the friction equation gives:
Mgsinθ=μ(Mgcosθ)
Cancelling Mg from both sides (assuming M≠0):
sinθ=μcosθ
Step 7: Solve for θ
Dividing both sides by cosθ:
tanθ=μ
Thus, the maximum angle θ for which the crate does not topple is given by:
θ=tan−1(μ)
Final Answer
The maximum angle θ for which the crate does not topple is:
θ=tan−1(μ)
---
The crate experiences several forces:
- The gravitational force Mg acting downwards at its center of mass.
- The normal force R2 acting perpendicular to the surface of the ramp.
- The frictional force F acting parallel to the surface of the ramp.
The crate will begin to topple when the normal force R1 at the edge of the ramp becomes zero. At this point, the torque due to the weight of the crate about the edge of the ramp will be balanced by the torque due to friction.
In the FBD, we can break down the weight of the crate into two components:
- The component parallel to the ramp: Mgsinθ
- The component perpendicular to the ramp: Mgcosθ
Taking torques about the edge of the ramp (where R1=0):
- The torque due to R2 (which is acting upwards) is R2⋅L2.
- The torque due to the weight of the crate (acting downwards) is Mgcosθ⋅L2.
R2⋅L2=Mgcosθ⋅L2
The frictional force can be expressed as:
F=μR2
Since F must balance the component of the weight acting down the ramp:
Mgsinθ=μR2
From the torque equation, we can express R2:
R2=Mgcosθ
Substituting this into the friction equation gives:
Mgsinθ=μ(Mgcosθ)
Cancelling Mg from both sides (assuming M≠0):
sinθ=μcosθ
Dividing both sides by cosθ:
tanθ=μ
Thus, the maximum angle θ for which the crate does not topple is given by:
θ=tan−1(μ)
The maximum angle θ for which the crate does not topple is:
θ=tan−1(μ)
Topper's Solved these Questions
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - EXAMPLE
1 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
Similar Questions
The centre in figure has dimensions m by h and the ramp is inclined at θ to the horizontal. Find the effective point of application of the normal force →n.
View SolutionTwo blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.
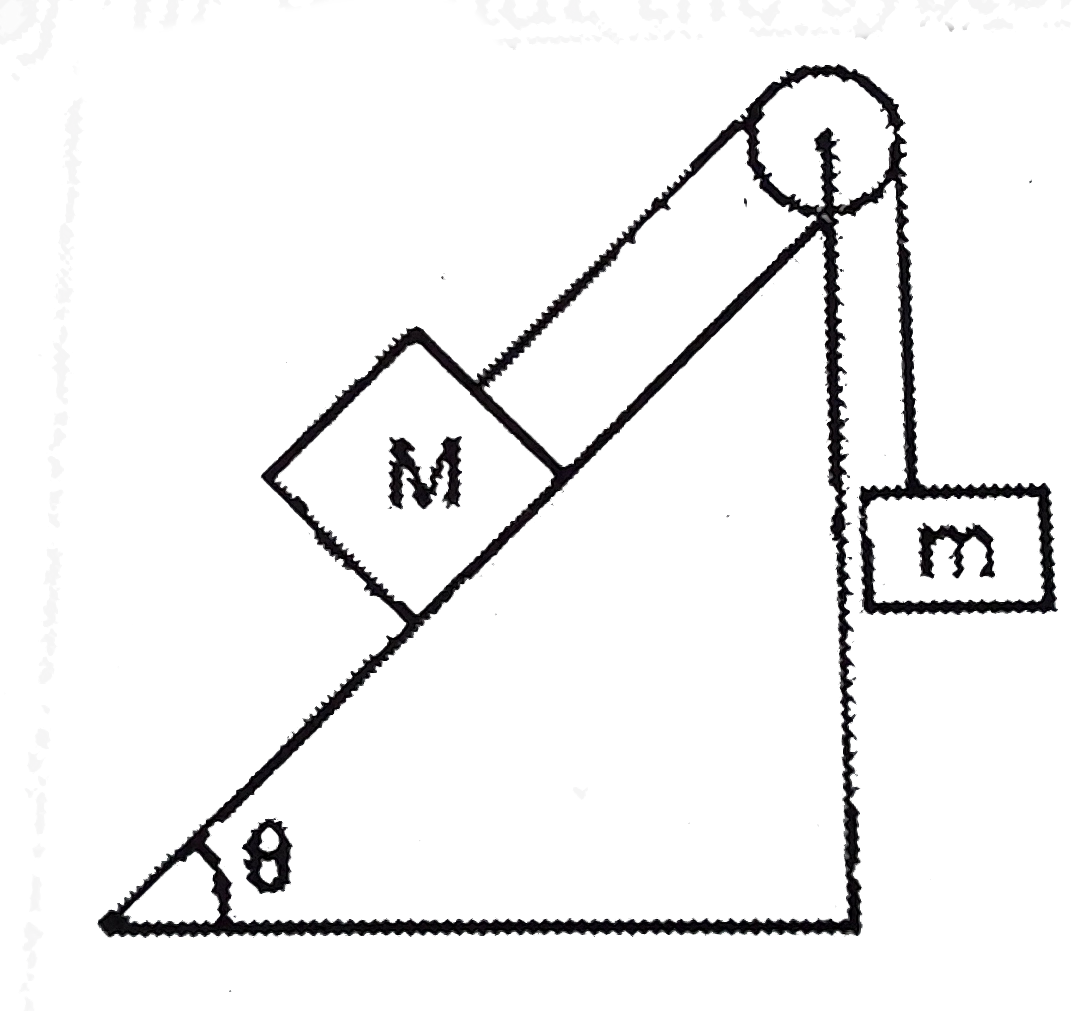
View Solution
Knowledge Check
A block of mass m is being pulled up the rough incline , inclined at angle θ with horizontal by an agent delivering constant power P. The coefficient of friction between block & incline is μ. Then during the upward motion along the inclined plane , maximum velocity of the block will be :
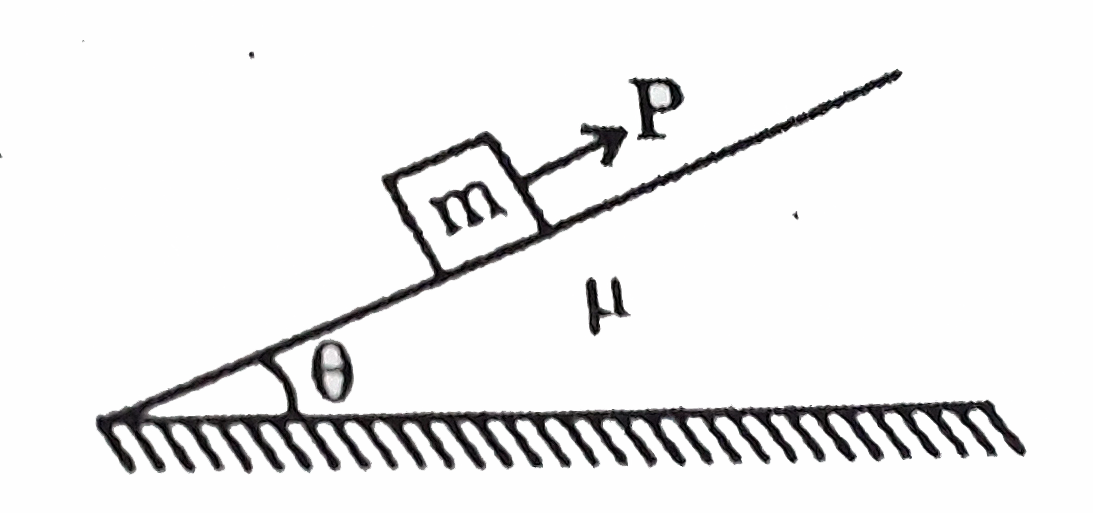 APmgsinθ+μ mgcosθBPmgsinθ−μ mgcosθCPmgsinθDPμmg sinθ
APmgsinθ+μ mgcosθBPmgsinθ−μ mgcosθCPmgsinθDPμmg sinθA man drags an m kg crate across a floor by pulling on a rope inclined at angle θ above the horizontal. If the coefficient of static friction between the floor and crate is then the tension required in the rope to start the crate moving is :
Aμsmg(sinθ−μscosθ)Bμsmg(sinθ+μscosθ)Cμsmg(cosθ−μssinθ)Dμsmg(cosθ+μssinθ)A solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.
A crate, in the form of a cube with edge lengths of 1.2 m, contains a piece of machinery, the center of mass of the crate and its contents is located 0.30 m above the crate's geometrical center. The crate rests on a ramp that makes an angle θ with the horizontal. As θ is increased from zero, an angle will be reached at which the crate will either tip over or start to slide down the ramp. If the coefficient of static friction between ramp and crate is 0.30, (a) does the crate tip or slide and (b) at what angle θ does this occur? If μs=0.70, (c) does the crate tip or slide and (d) at what angle θ does this occur? (Hint: At the onset of tipping, where is the normal force located?)
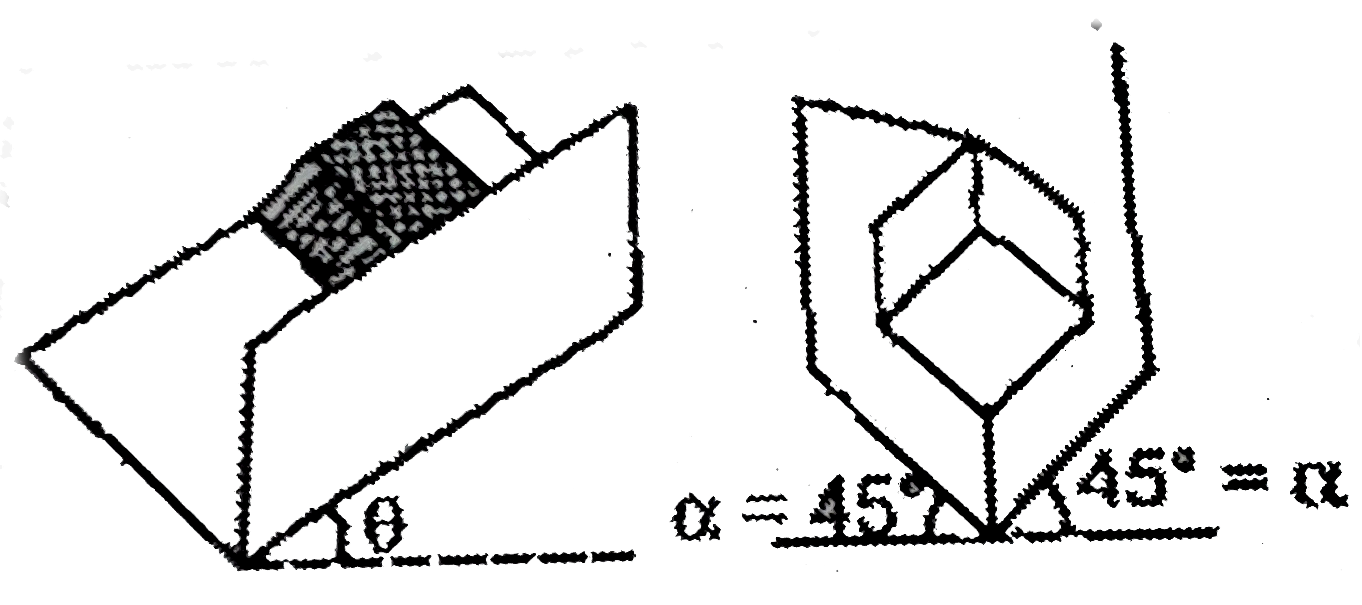
View SolutionA wooden block slides down the right angle channel as shown in Fig. The channel is inclined at an angle θ w.r.t. the horizontal . The angle α is 45∘, i.e., the channel is oriented symmetrically with the vertical. IF the coefficient of friction between the block and the channel is μk, find the acceleration of the block.
View SolutionA crate is pulled along a horizontal surface at constant velocity by an applied force F that makes an angle θ with the horizontal. The coefficient of kinetic friction between the crate and the surface is μ. Find the angle θ such that the applied force is minimum to slide the block. Also find the minimum value of this force.
View SolutionA hollow sphere rolls down a rough inclined plane whose angle of inclination is θ, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [μ = coefficient of friction between the hollow sphere and inclined plane]
View SolutionA uniform cylinder of height h and radius r is placed with its circular face on a rough inclined plane and the inclination of the plane to the horizontal is gradually increased. If μ is the coefficient of friction, then under what condition the cylinder will (a) slide before toppling (b) topple before sliding.
View Solution
