Question

The centre in figure has dimensions $m$ by $h$ and the ramp is inclined at $\theta$ to the horizontal. Find the effective point of application of the normal force $\overrightarrow{n}$.

Explanation

Problem solving strategy : The crate is in equilibrium. By appliying force and torque balance, we may find where the normal force acts.

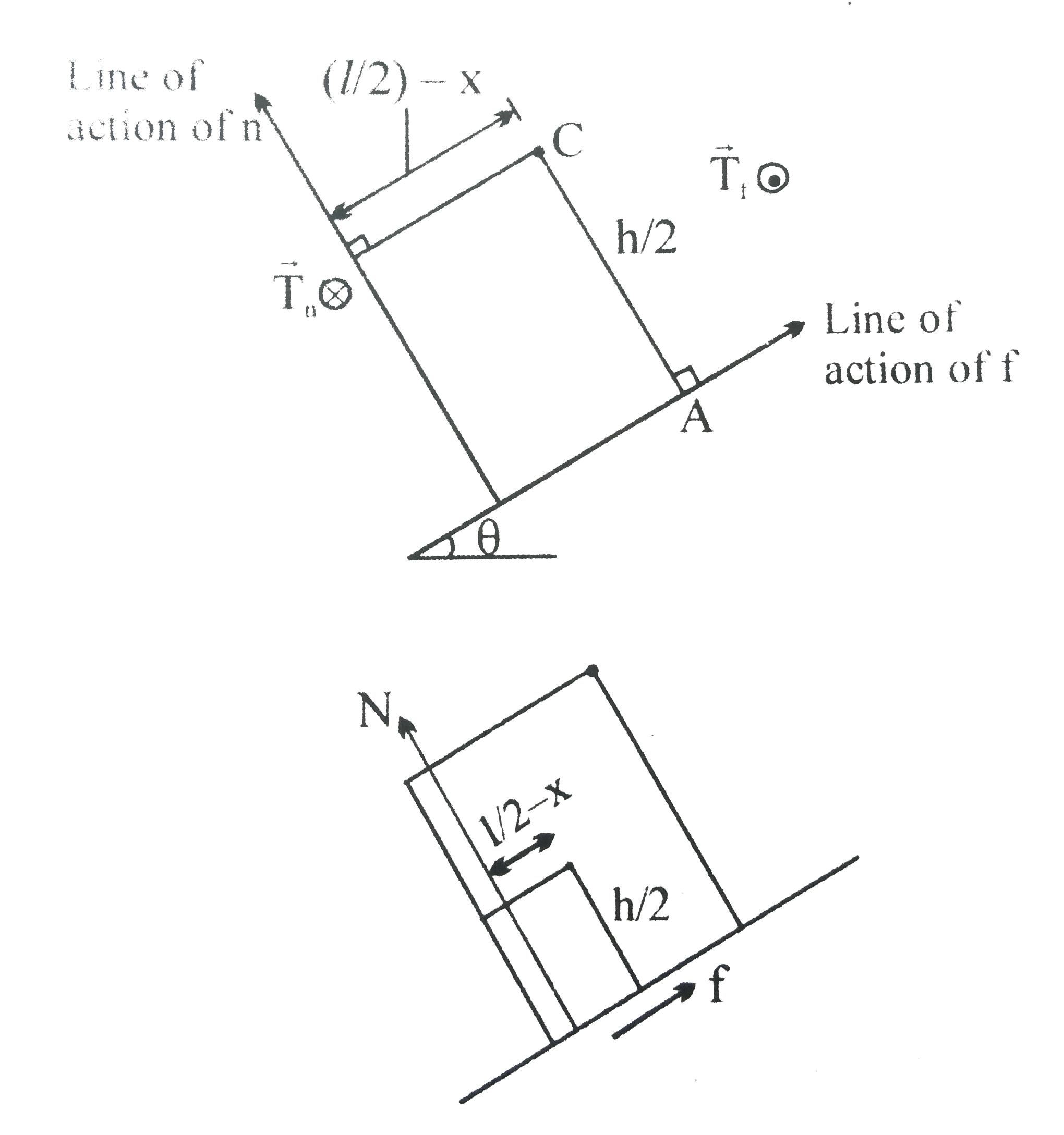
We choose the x-axis to be along the slope and the y-axis to be perpendicular to it. The sum of force compounds in each direaction must be zero.
`0 = Sigma F_(x) = f - W sin theta`
and `0 = Sigma F_(y) = n - W cos theta`
Three force exert torque :
(1) The weight acts at the `CM` and so exerts no torque about it.
(2) The friction force acts along the surface between crate and ramp and exerts on toque `f h//2`, out of the paper (figure).
(3) The normal force acts at an unknown distance `x` from the downhill edge of teh crate and exerts a torque `n[(1//2) -x]` into the page.
These torque sum to zero
`0 = Sigma vec tau[f(h//2) - n {(l//2) -x] hat k` (out of the page).
From force balance, we have `f = W sin theta` and `N = W cos theta`
so `W sin (h//2) = W cos[(l//2) - x]`
The above equation may be solved for `x`.
`Sigma vec tau = 0`.