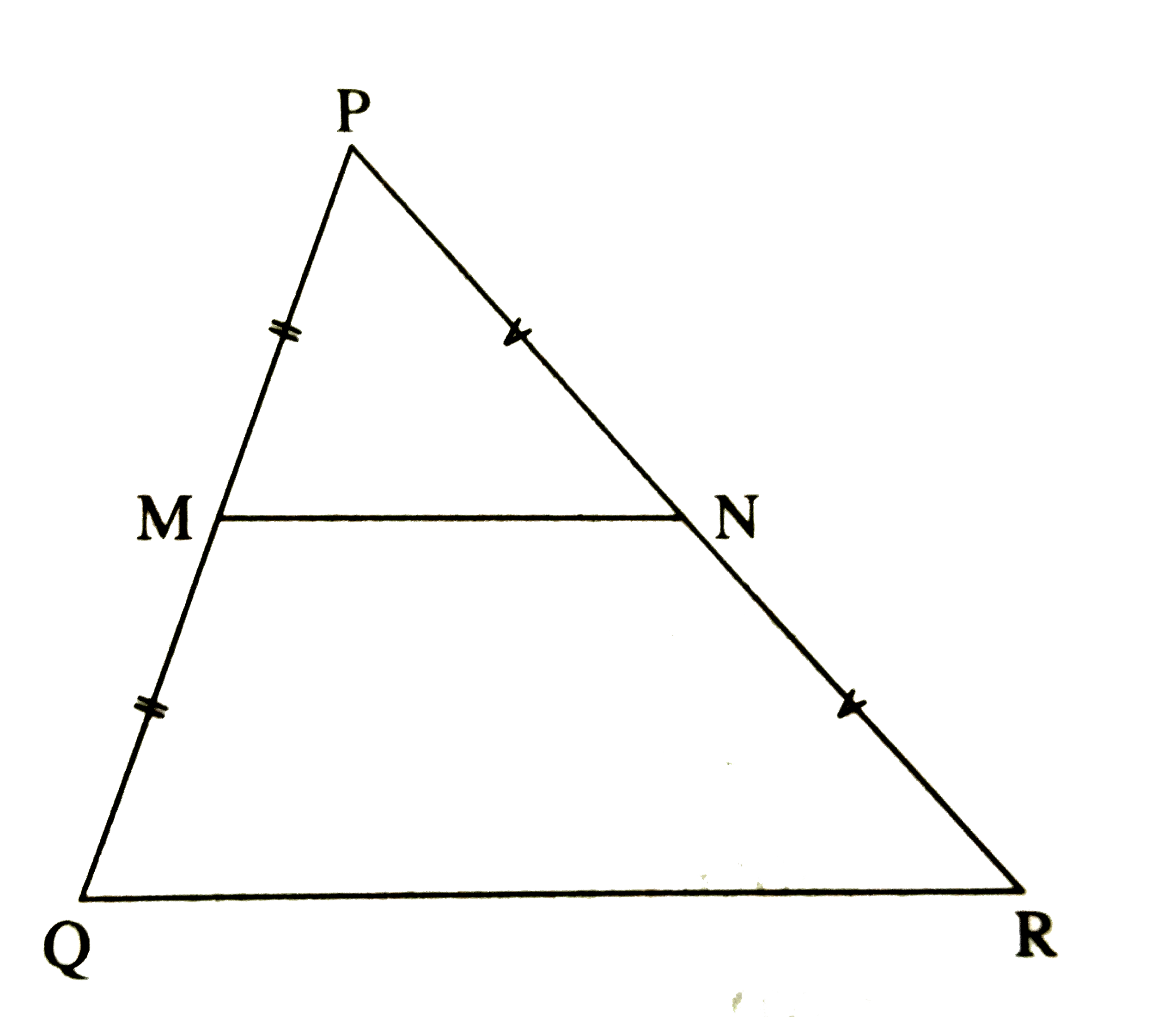
In ΔPQR,PQ=PR=18cm, AB and AC are parallel to lines PR and PQ respectively. If A is the mid-point of QR, then what is the perimeter (in cm) of quadrilateral ABPC?
18
28
32
36
The correct Answer is:D
To solve the problem, we need to find the perimeter of quadrilateral ABPC in triangle PQR where PQ = PR = 18 cm and A is the midpoint of QR. Lines AB and AC are parallel to PR and PQ, respectively.
1. Draw Triangle PQR:
- Start by drawing triangle PQR with points P, Q, and R.
- Since PQ = PR = 18 cm, label PQ and PR as 18 cm each.
2. Identify Midpoint A:
- Mark point A as the midpoint of side QR. This means that the length of QA = AR.
3. Draw Parallel Lines:
- Draw line AB parallel to line PR and line AC parallel to line PQ. Since A is the midpoint of QR, lines AB and AC will also divide the triangle into smaller triangles.
4. Apply Midpoint Theorem:
- By the midpoint theorem, since A is the midpoint of QR, the length of AB will be half of PR.
- Therefore, AB=12×PR=12×18 cm=9 cm.
5. Calculate Length of AC:
- Similarly, since A is the midpoint of QR and AC is parallel to PQ, the length of AC will also be half of PQ.
- Thus, AC=12×PQ=12×18 cm=9 cm.
6. Determine Lengths of PB and PC:
- Since A is the midpoint of QR, and AB and AC are parallel to the sides of the triangle, the lengths PB and PC will be equal to the lengths of AB and AC respectively.
- Therefore, PB=9 cm and PC=9 cm.
7. Calculate the Perimeter of Quadrilateral ABPC:
- The perimeter of quadrilateral ABPC can be calculated by adding the lengths of all its sides:
Perimeter=AB+BP+PC+AC=9 cm+9 cm+9 cm+9 cm=36 cm.
Final Answer:
The perimeter of quadrilateral ABPC is 36 cm.
- Start by drawing triangle PQR with points P, Q, and R.
- Since PQ = PR = 18 cm, label PQ and PR as 18 cm each.
- Mark point A as the midpoint of side QR. This means that the length of QA = AR.
- Draw line AB parallel to line PR and line AC parallel to line PQ. Since A is the midpoint of QR, lines AB and AC will also divide the triangle into smaller triangles.
- By the midpoint theorem, since A is the midpoint of QR, the length of AB will be half of PR.
- Therefore, AB=12×PR=12×18 cm=9 cm.
- Similarly, since A is the midpoint of QR and AC is parallel to PQ, the length of AC will also be half of PQ.
- Thus, AC=12×PQ=12×18 cm=9 cm.
- Since A is the midpoint of QR, and AB and AC are parallel to the sides of the triangle, the lengths PB and PC will be equal to the lengths of AB and AC respectively.
- Therefore, PB=9 cm and PC=9 cm.
- The perimeter of quadrilateral ABPC can be calculated by adding the lengths of all its sides:
Perimeter=AB+BP+PC+AC=9 cm+9 cm+9 cm+9 cm=36 cm.
The perimeter of quadrilateral ABPC is 36 cm.
Similar Questions
Knowledge Check
In ΔPQR,SandT are the mid points of sides PQ and PR respectively. If ∠QPR=45∘and∠PRQ=55∘, then what is the value (in degrees) of ∠QST ?
A80B85C90D100In ΔPQR, a line parallel to side QR cuts the side PQ and PR at points M and N respectively and point M divide PQ in the ratio of 1 : 2. If area of ΔPQR is 360 cm2, then what is the area (in cm2) of quadrilateral MNRQ?
A160B320C120D96ΔPQR is right angled at point Q. If PQ=8cmand PR=(QR+2)cm. What is the value (in cm) of PR?
A17B15C19D18
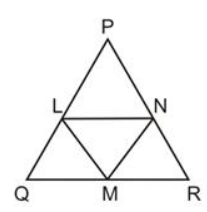
In A PQR, if PQ=PQ and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
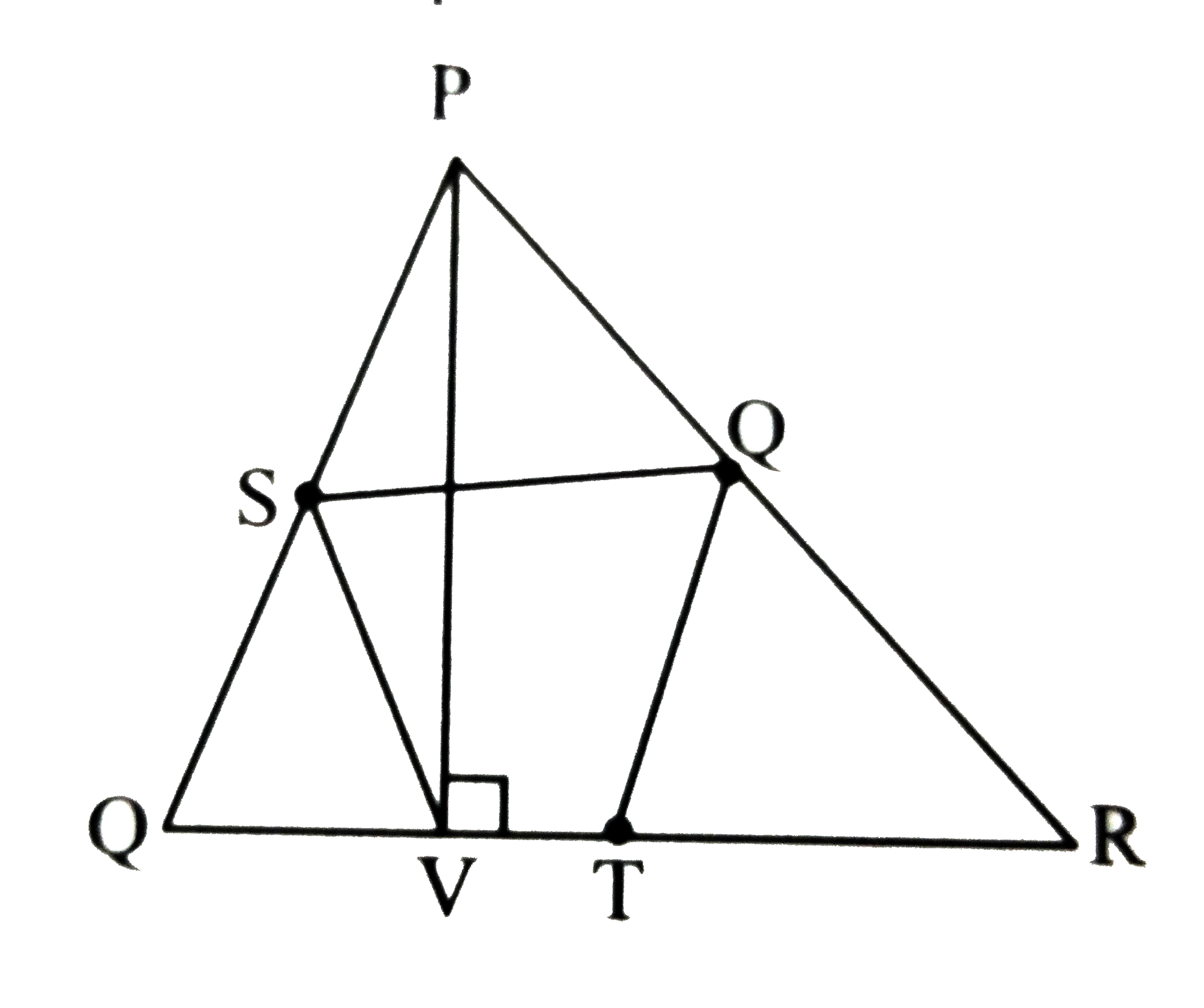
View SolutionIn the given figure, points S,T and U are the midpoints of sides PQ,QR and PR respectively. IF PV⊥QR, then prove that □ SVTU is a cyclic quadrilateral.
View SolutionIn ΔPQR,PQ=6√3cm,PR=12cmandQR=6cm then ∠Q is
View SolutionPQR is an isosceles triangle with sides PQ=PR=45cmand QR=72cm. PN is a median to base QR. What will be the length (in cm.) of PN?
View SolutionPQR is an isosceles triangle with sides PQ=PR=45cmand QR=72cm. PN is a median to base QR. What will be the length (in cm.) of PN?
View Solution