O is the centre of the circle and two tangents are drawn from a point P to this circle at points A and B. If ∠AOP=50∘, then what is the value (in degrees) of ∠APB?
60
80
90
100
The correct Answer is:B
Step by step video, text & image solution for O is the centre of the circle and two tangents are drawn from a point P to this circle at points A and B. If angleAOP=50^(@), then what is the value (in degrees) of angleAPB? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Two tangents are drawn from a point P to a circle at Q and R. If O is the centre of the circle and ∠QOP=40∘, then what is the value (in degrees) of ∠QPR?
A60B80C90D100 - Question 2 - Select One
Two tangents are drawn from a point P to a circle at A and B. O is the centre of the circle. If ∠AOP=60∘, then ∠APB is
A120∘B90∘C60∘D30∘ - Question 3 - Select One
XR is a tangent to the circle. O is the centre of the circle. If ∠XRP=120∘, then what is the value (in degrees) of ∠QOR?
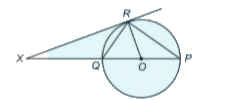 A80B70C60D40
A80B70C60D40
O is the centre of the circle. A tangent is drawn which touches the cirlce at C. If ∠AOC=80∘, then what is the value (in degrees) of ∠BCX?
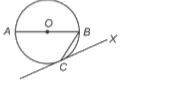 View Solution
View SolutionIn figure, PTandPS are tangents drawn from a point P to a circle with centre at 0. If ∠OPT=35∘, find aandb.
View SolutionTheorem: The length of two tangents drawn from an external point to a circle are equal.
View SolutionThe centre of the circle is O. Two tangents are drawn from the point of the circle A & B, which meets at the point P. Accordingly if ∠AOB=120∘, then find out the ratio of ∠APB:∠AOP?
View SolutionIf angle between two tangents drawn from a point P to a circle of radius 'a' and the centre O is 90∘ then prove that OP=√a
View Solution
