P is a point outside the circle at a distance of cm from centre O of the circle . PR be a secant such that it intersects the circle at Q and R . If cm and cm , then what is the radius ( in cm ) of the circle ?
The correct Answer is:3
To find the radius of the circle given the distances and segments, we can use the secant-tangent theorem. Here’s how to solve the problem step by step:
1. Identify the Given Values:
- Distance from point P to the center O of the circle: PO=6.5 cm.
- Length of segment PQ: PQ=4.5 cm.
- Length of segment QR: QR=3.5 cm.
2. Calculate the Length of PR:
- Since PR=PQ+QR:
PR=4.5cm+3.5cm=8cm.
3. Set Up the Secant-Tangent Theorem:
- According to the secant-tangent theorem, we have:
PQ×PR=PO2−r2,
where r is the radius of the circle.
4. Substitute the Known Values:
- Substitute PQ=4.5 cm, PR=8 cm, and PO=6.5 cm into the equation:
4.5×8=6.52−r2.
5. Calculate the Left Side:
- Calculate 4.5×8:
4.5×8=36.
6. Calculate 6.52:
- Calculate 6.52:
6.52=42.25.
7. Set Up the Equation:
- Now we have:
36=42.25−r2.
8. Rearranging the Equation:
- Rearranging gives:
r2=42.25−36.
- Simplifying:
r2=6.25.
9. Taking the Square Root:
- Taking the square root of both sides gives:
r=√6.25=2.5cm.
Conclusion
The radius of the circle is 2.5 cm.
- Distance from point P to the center O of the circle: PO=6.5 cm.
- Length of segment PQ: PQ=4.5 cm.
- Length of segment QR: QR=3.5 cm.
- Since PR=PQ+QR:
PR=4.5cm+3.5cm=8cm.
- According to the secant-tangent theorem, we have:
PQ×PR=PO2−r2,
where r is the radius of the circle.
- Substitute PQ=4.5 cm, PR=8 cm, and PO=6.5 cm into the equation:
4.5×8=6.52−r2.
- Calculate 4.5×8:
4.5×8=36.
- Calculate 6.52:
6.52=42.25.
- Now we have:
36=42.25−r2.
- Rearranging gives:
r2=42.25−36.
- Simplifying:
r2=6.25.
- Taking the square root of both sides gives:
r=√6.25=2.5cm.
The radius of the circle is 2.5 cm.
Similar Questions
The length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What will be the radius of the circle ?
View SolutionDraw a circle of radius 3.5 cm. Take a point P outside the circle at a distance of 7 cm from the centre of the circle and construct a pair of tangents to the circle from the point.
View Solution
Knowledge Check
In ΔPQR,∠PQR=90∘,PQ=5cmandQR=12cm. What is the radius (in cm) of the circum-circle of ΔPQR?
A6.5B7.5C13D15In ΔPQR,∠PQR=90∘,PQ=5cmandQR=12cm. What is the radius (in cm) of the circum-circle of ΔPQR?
A6.5B7.5C13D15In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at N and R. PQ=15cm,PR=25cm, find PN:
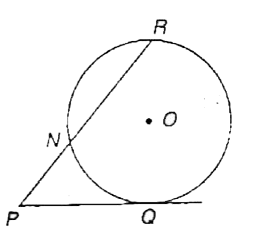 A15 cmB10 cmC9 cmD6 cm
A15 cmB10 cmC9 cmD6 cm
The length of tangent from a point A at a distance of 12 cm from the centre of the circle is 9 cm. What is the radius of the circle ?
View SolutionA chord of length 60 cm is at a distance of 16 cm from the centre of a circle . What is the radius (in cm ) of the circle ?
View SolutionA chord of length 120 cm is at a distance of 32 cm from the centre of a circle. What is the radius (in cm) of the circle?
View SolutionA chord of length 120 cm is at a distance of 32 cm from the centre of a circle. What is the radius (in cm) of the circle?
View SolutionP is a point outside a circle and is 26cm away from its centre.A secant PAB drawn from intersects the circle at points A and B such that PB = 32 cm and PA = 18 cm. The radius of the circle ( in cm ) is :
View Solution
