Two identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameters, and the force between them is F. A third identical conducting spheres, C,is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to :
3F4
F2
F
3F8
The correct Answer is:D
Spheres A and B carry equal charge say .q.
∴ Force between them , F=kqqr2
When A and C are touched, charge on both qA=qC=q2
Then when B
qB=q2+q23q4
Now, the force between charge qAandqB
F.=kqAqBr2=k×q2×3q4r2=38kq2r2=38F
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 1 Concept builder (Topicwise)
58 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator
24 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE -2 : CONCEPT ALLPLICATOR
30 Videos
- ELECTROMAGNETIC INDUCTION BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 2 : Concept Applicator
29 Videos
Similar Questions
Two small conducting spheres have charges 2.1nC and −0.1nCare touched to each other and then separated by a distance of 0.5 m. Find the force between them
View SolutionTwo identical conducting spheres 1 and 2 carry equal amounts of charge and are ficed apart at a certain distance larger than their diameters. The spheres repel each other with an electrical force of 88mN. A thired identical sphere 3, having an insulating handle and initially uncharged, is touched first to sphere 1 and then to sphere 2 and finally removed. Find the force between spheres 1 and 2 as shown if Figure.
 ,
,
View Solution
Knowledge Check
Two identical non-conducting spheres having charges of -12 nC and + 8 nC are touched together and then separated. The 3 nal charge on each is
A−2ncB−(23)ncC+2nCD+4nCTwo conducting spheres of radii R each are given equal charges +Q and are kept such that their centre are at distance r (≥R). The force of attraction (F) between them is:
AKQ2r2BKQ2(r+2R)2CKQ2r2≥F≥KQ2(r−2R)2≥F≥KQr2DKQ2(r−2R)2gtFgtKQr2A conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
AQ/4BQ/3CQ/2D2Q/3
Two identical conducting spheres are charged by induction and then sepatatd by a large distance, sphere-1 has charge +Q and spher-2 has charge -Q. A third sphere is initially uncharged. If sphere-3 is touched to sphere-1 and sepatated and then touched to sphere-2 and separated what is the final charge on each of the three spheres?
View SolutionTwo identical spheres each of mass M and radius R are separated by a distance 3R. The force of attraction between them is proportional to
View SolutionIndentical isolated conduction sphers 1 and 2 have equal charges and are separated by a distance that is large compared with their diameters (Fig.a). The electrostatic force acting on spkhere 2 due to sphere 1 is F. Suppose now that a third identical sphere 3, having an insulation handle and initially neutral, is touched first to sphere 1 (Fig. b), then to sphere 2 (Fig. c), and dinally removed (Fig. d). The electrostatic force that now acts on sphere 2 has magnitude F'. What is the F'F?
View SolutionThere are two charged identical metal spheres A and B repel each other with a force 3×10−5N. Another identical uncharged sphere C is touched with A and then placed at the mid-point between A and B. Net force on C is
View SolutionIn Frame 1, two identical conducting spheres, A and B, carry equal amounts of excess charge that have the same sign. The spheres are separated by a distance d, and sphere A exerts an electrostatic force on sphere B that has a magnitude F. A third sphere, C, Which is handled only by an insulating rod, is introduced in Frame 2. Sphere C is identical to A and B except that it initially uncharged. Sphere C is touched first to sphere A, in Frame 2, and then to sphere B, in Frame 3, and is finally removed in Frame 4.
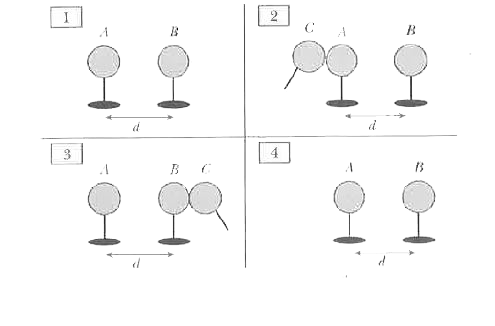
Determine the magnitude of the electrostatic force that sphere A exerts on sphere B in Frame 4.
View Solution
