ABCD is a cyclic trapezium with AB || DC and AB = diameter of the circle. If ∠CAB=30∘, then ∠ADC is
60∘
120∘
150∘
30∘
The correct Answer is:B
To solve the problem, we will use the properties of cyclic trapeziums and the angles formed by the diameter of the circle.
1. Understanding the Configuration:
- We have a cyclic trapezium ABCD where AB is parallel to DC and AB is the diameter of the circle.
- Since AB is the diameter, angle ACB is a right angle (90 degrees) according to the inscribed angle theorem.
2. Identifying Given Angles:
- We are given that angle CAB = 30 degrees.
3. Finding Angle ABC:
- In triangle ABC, we know that the sum of angles in a triangle is 180 degrees.
- Therefore, angle ABC can be calculated as:
angle ABC=180∘−angle CAB−angle ACB
angle ABC=180∘−30∘−90∘=60∘
4. Using the Properties of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, the opposite angles are supplementary. Thus, angle ABC + angle ADC = 180 degrees.
- We already found that angle ABC = 60 degrees.
5. Calculating Angle ADC:
- Using the supplementary angle property:
angle ADC=180∘−angle ABC
angle ADC=180∘−60∘=120∘
Final Answer:
Thus, angle ADC is 120 degrees.
- We have a cyclic trapezium ABCD where AB is parallel to DC and AB is the diameter of the circle.
- Since AB is the diameter, angle ACB is a right angle (90 degrees) according to the inscribed angle theorem.
- We are given that angle CAB = 30 degrees.
- In triangle ABC, we know that the sum of angles in a triangle is 180 degrees.
- Therefore, angle ABC can be calculated as:
angle ABC=180∘−angle CAB−angle ACB
angle ABC=180∘−30∘−90∘=60∘
- In a cyclic quadrilateral, the opposite angles are supplementary. Thus, angle ABC + angle ADC = 180 degrees.
- We already found that angle ABC = 60 degrees.
- Using the supplementary angle property:
angle ADC=180∘−angle ABC
angle ADC=180∘−60∘=120∘
Thus, angle ADC is 120 degrees.
Similar Questions
In the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
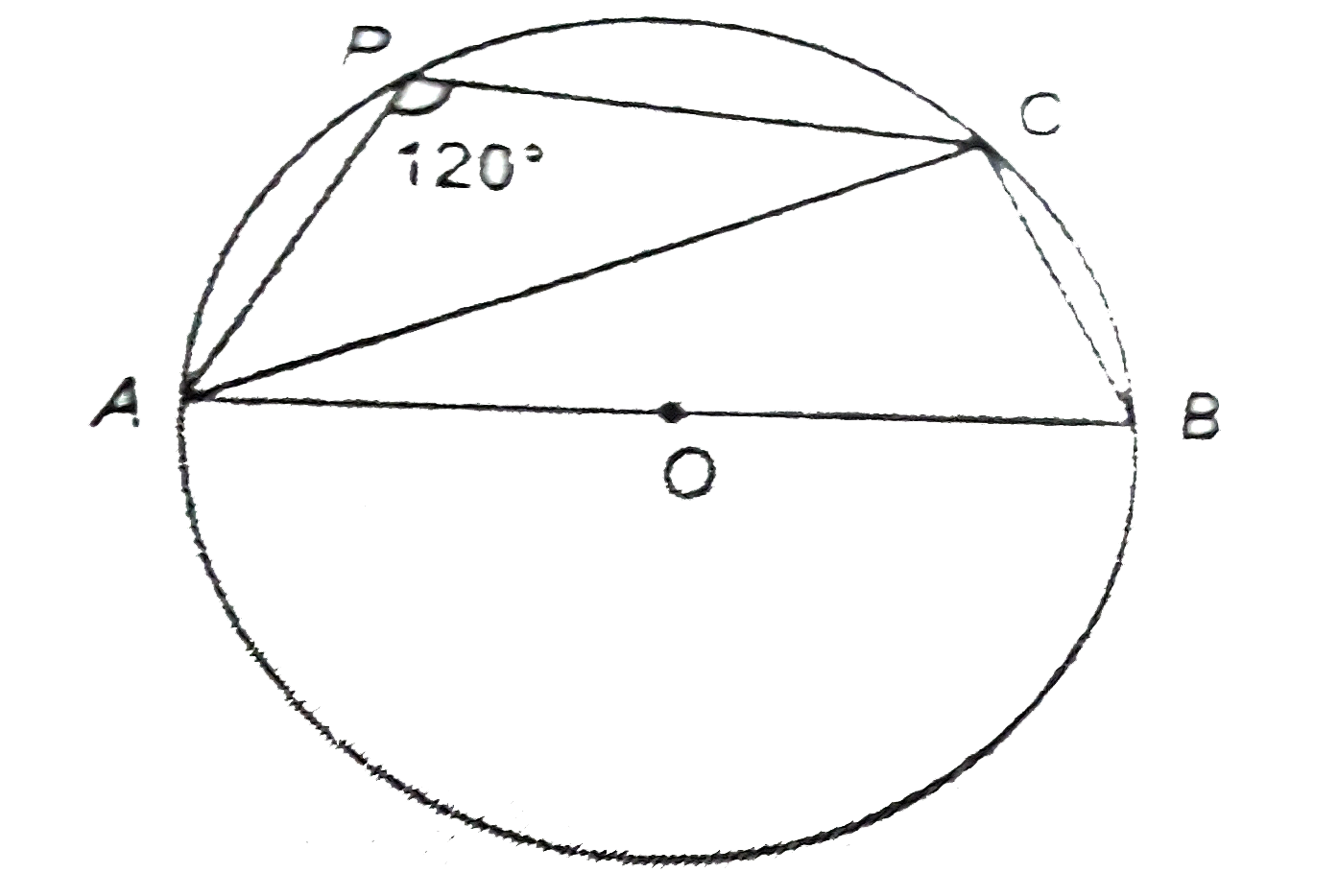
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View Solution
Knowledge Check
ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠CAB=48∘, then what is the value (in degrees) of ∠ADC?
A52B77C138D142ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, then ∠BAC is equal to
A80∘B50∘C40∘D30∘ABCD is a cyclic quadrilateral such that AB is diameter of the circle circumscirbing it and angle ADC=126∘.∠BAC is equal to
A72∘B36∘C18∘D24∘
ABCD is a cyclic trapezium & ABII CD, AB is diameter. BC = 2cm, AB = 8 cm, CD = ?
View SolutionABCD is a cyclic trapezium , in which AB||DC. If ∠B=75∘ , then find other angles.
View SolutionABCD is a cyclic trapezium & AB is diameter. BC = 2cm, AB = 8 cm, CD = ?
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC=130∘ . Then angle BAC is equal to:
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC = 140∘, ∠BAC is equal to:
ABCD एक चक्रीय चतुर्भज है जो इस प्रकार है कि AB इसे घेरने वाले वृत्त का व्यास है तथा कोण ADC = 140∘, है | कोण ∠BAC किसके बराबर है?
View Solution
