ABCD is a cyclic trapezium & AB is diameter. BC = 2cm, AB = 8 cm, CD = ?
7
6.5
6
7.5
To solve the problem, we need to find the length of CD in the cyclic trapezium ABCD, where AB is the diameter and given that BC = 2 cm and AB = 8 cm.
1. Identify the Given Information:
- AB (diameter) = 8 cm
- BC = 2 cm
- Since AB is the diameter, we can conclude that the center of the circle is at the midpoint of AB.
2. Calculate the Radius:
- The radius (r) of the circle is half of the diameter:
r=AB2=82=4 cm
3. Use the Properties of Cyclic Trapezium:
- In a cyclic trapezium, the angles subtended by the same chord are equal. Since AB is the diameter, angle ACB is a right angle (90 degrees).
4. Apply Pythagorean Theorem in Triangle ACB:
- In triangle ACB, we can use the Pythagorean theorem:
AC2+BC2=AB2
- Let AC = x. Thus, we have:
x2+(2)2=(8)2
x2+4=64
x2=64−4=60
x=√60=2√15 cm
5. Calculate the Length of CD:
- Since ABCD is a trapezium, we can use the property that the sum of the lengths of the bases (AB and CD) equals the sum of the lengths of the non-parallel sides (BC and AD).
- We know AB = 8 cm and BC = 2 cm. Let CD = y.
- The relationship can be expressed as:
AB+CD=BC+AD
- Since AD is equal to BC in a cyclic trapezium, we can substitute:
8+y=2+2
8+y=4
y=4−8=−4 (not possible)
- We need to re-evaluate the relationship. The correct relationship would be:
AB−CD=BC+AD
- Thus:
8−y=2+2
8−y=4
y=8−4=4 cm
Final Answer:
CD = 4 cm
- AB (diameter) = 8 cm
- BC = 2 cm
- Since AB is the diameter, we can conclude that the center of the circle is at the midpoint of AB.
- The radius (r) of the circle is half of the diameter:
r=AB2=82=4 cm
- In a cyclic trapezium, the angles subtended by the same chord are equal. Since AB is the diameter, angle ACB is a right angle (90 degrees).
- In triangle ACB, we can use the Pythagorean theorem:
AC2+BC2=AB2
- Let AC = x. Thus, we have:
x2+(2)2=(8)2
x2+4=64
x2=64−4=60
x=√60=2√15 cm
- Since ABCD is a trapezium, we can use the property that the sum of the lengths of the bases (AB and CD) equals the sum of the lengths of the non-parallel sides (BC and AD).
- We know AB = 8 cm and BC = 2 cm. Let CD = y.
- The relationship can be expressed as:
AB+CD=BC+AD
- Since AD is equal to BC in a cyclic trapezium, we can substitute:
8+y=2+2
8+y=4
y=4−8=−4 (not possible)
- We need to re-evaluate the relationship. The correct relationship would be:
AB−CD=BC+AD
- Thus:
8−y=2+2
8−y=4
y=8−4=4 cm
CD = 4 cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
A80∘B100∘C120∘D140∘ABCD is a cyclic quadrilateral in which AB= 16.5 cm, BC = x cm, CD = 11 cm, AD= 19.8 cm and BD is bisected by AC at O. What is the value of x?/
ABCD एक चक्रीय चतुर्भुज है जिसमें AB = 16.5 सेमी, BC = x सेमी, CD = 11 सेमी, AD = 19.8 सेमी है तथा BD को AC के द्वारा O पर समद्विभाजित किया जाता है | x का मान क्या है ?A13.8 cmB12.4 cmC12.8 cmD13.2 cmABCD is a cyclic quadrilateral in which AB is a diameter, BC = CD and ∠A=50∘ then ∠DBC is :
A25∘B20∘C45∘D30∘
ABCD is a trapezium in which AD||BC, AB = 9 cm BC = 12 cm CD = 15 cm DA = 30 cm find the sum of diagonals's square
View SolutionABCD is a trapezium in which AD II BC . AB = 9 cm, BC =12 cm, CD = 15 cm, DA = 20 cm. Find the sum of square of diagonals.
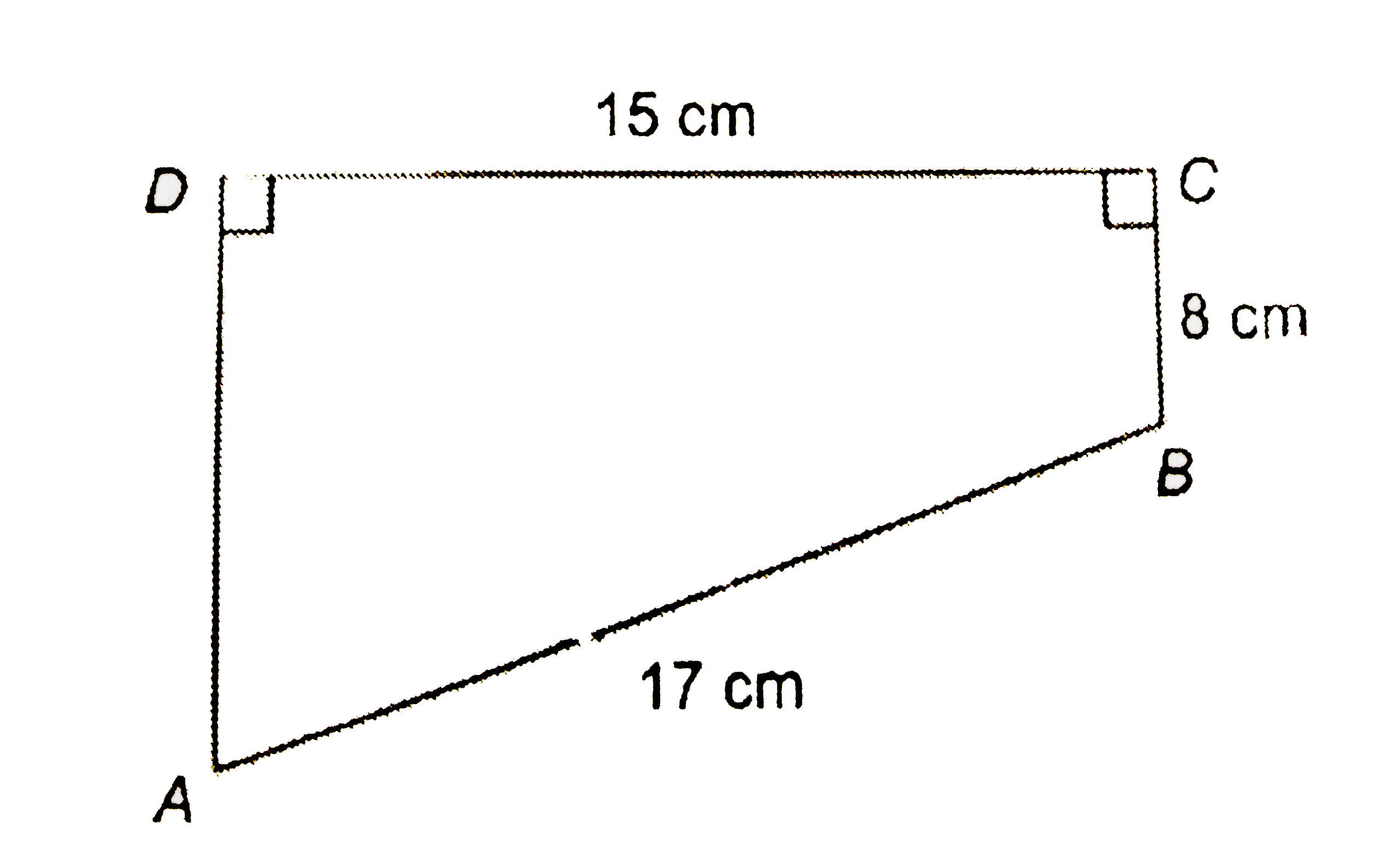
View SolutionThe given figure shows a trapezium ABCD in which AB = 17 cm, BC = 8 cm and CD = 15 cm. Find the area of the trapezium.
View SolutionABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
View SolutionABCD is a cyclic quadrilateral in which AB = 15 cm, BC = 12 cm and CD = 10 cm. If AC bisects BD, then what is the measure of AD?
View Solution
