Ten particles are moving with the following speeds: four at 300 m/s, two at 500 m/s, and four at 600 m/s. Calculate their (a) average and (b)rms speeds. (c) Is vrms>vavg ?
To solve the problem, we need to calculate the average speed and the root mean square (RMS) speed of the ten particles moving at different speeds.
Step 1: Identify the speeds and their frequencies.
- We have 10 particles with the following speeds:
- 4 particles at 300 m/s
- 2 particles at 500 m/s
- 4 particles at 600 m/s
Step 2: Calculate the average speed (V_avg).
The average speed is calculated using the formula:
Vavg=V1+V2+V3+...+Vnn
Where n is the total number of particles.
Substituting the values:
Vavg=(4×300)+(2×500)+(4×600)10
Calculating the numerator:
=(1200)+(1000)+(2400)10=420010=420 m/s
Step 3: Calculate the root mean square speed (V_rms).
The RMS speed is calculated using the formula:
Vrms=√V21+V22+V23+...+V2nn
Substituting the values:
Vrms=√(4×3002)+(2×5002)+(4×6002)10
Calculating the squares:
=√(4×90000)+(2×250000)+(4×360000)10
Calculating the numerator:
=√(360000)+(500000)+(1440000)10=√200000010=√200000=447.21 m/s
Step 4: Compare V_rms and V_avg.
Now we compare the two speeds:
- Vavg=420 m/s
- Vrms=447.21 m/s
Since Vrms>Vavg, we conclude that the RMS speed is greater than the average speed.
Final Answers:
(a) Average speed Vavg=420 m/s
(b) RMS speed Vrms≈447.21 m/s
(c) Yes, Vrms>Vavg.
---
- We have 10 particles with the following speeds:
- 4 particles at 300 m/s
- 2 particles at 500 m/s
- 4 particles at 600 m/s
The average speed is calculated using the formula:
Vavg=V1+V2+V3+...+Vnn
Where n is the total number of particles.
Vavg=(4×300)+(2×500)+(4×600)10
Calculating the numerator:
=(1200)+(1000)+(2400)10=420010=420 m/s
The RMS speed is calculated using the formula:
Vrms=√V21+V22+V23+...+V2nn
Vrms=√(4×3002)+(2×5002)+(4×6002)10
Calculating the squares:
=√(4×90000)+(2×250000)+(4×360000)10
Calculating the numerator:
=√(360000)+(500000)+(1440000)10=√200000010=√200000=447.21 m/s
Now we compare the two speeds:
- Vavg=420 m/s
- Vrms=447.21 m/s
(a) Average speed Vavg=420 m/s
Topper's Solved these Questions
- THE KINETIC THEORY OF GASESBOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type )
1 Videos
- THE KINETIC THEORY OF GASESBOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS
72 Videos
- THE KINETIC THEORY OF GASESBOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - CHECK POINT
2 Videos
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( INTEGER TYPE )
3 Videos
- THE NUCLEUSBOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PRACTICE QUESTIONS(Integer Type)
7 Videos
Similar Questions
A particle moves in a straight line with constant speed of 4m/s for 2s, then with 6m/s for 3s. Find the average speed of the particle in the given time interval.
View SolutionFive gas molecules chosen at random are found to have speed of 500,600,700,800and900m/s. Find the rms speed. Is it the same as the average speed ?
View Solution
Knowledge Check
A particle is moving in a circle of radius 1 m with speed varying with time as v=(2t)m/s. In first 2 s
Adistance travelled by the particle is 4mBdisplacement of the particle is 2 sin 2Caverage speed of the particle is 2 m/sDaverage velocity of the particle is zeroA car moves a distance of 100 m. It coveres first half with speed of 10 m/s and another half with speed of v m/s. If the average speed of car is 18 m/s, then value of v is
A60 m/sB80 m/sC90 m/sD110 m/sThe ratio of average speed of an oxygen molecule to the r.m.s. speed of a N2 molecule at the same temperature is :
A(3π7)1/2B(73π)1/2C(37π)1/2D(7π3)12
Consider an 1100 particels gas system with speeds distribution as follows :
1000 particles each with speed 100m/s
2000 particles each wityh speed 200m/s
4000 particles each with speed 300m/s
3000 particles each with speed 400m/s and 1000 particles each with speed 500m/s
Find the average speed, and rms speed.
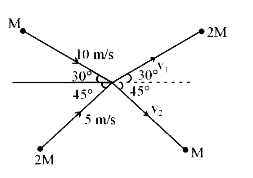
View SolutionTwo particles of masses M and 2M, moving as shown, with speeds of 10 m/s and 5 m/s, collide elastically at the origin. After the collision, they move along the indicated diretions with speeds v1 and v2 respectively. The value of v1 and v2 are nearly:
View SolutionTwo tuning forks A and B having a frequency of 500 Hz each are placed with B to the right of A. An observer in between the forks in moving towards B with a speed of 25 m/s. The speed of sound is 345 m/s and the wind speed is 5 m/s from A to B. Calculate the difference in the two frequencies heard by observer.
View SolutionExplain why the speed of sound through a gas cannot be greater than the r.m.s. speed of the molecules of the gas.
View SolutionThe average speed of gas molecules is 400 m/sec. Calculate its rms speed at the same temperature.
View Solution
