Consider the slabe shown in Figure. Suppose that L = 15.0 cm , A =105cm2, and the material is copper. If TH=125∘C,TC=10.0∘C, and a steady state is reached, find the conduction rate through the slabe.
To find the conduction rate through the slab, we will use Fourier's law of heat conduction, which states:
Q=k⋅A⋅(TH−TC)L
Where:
- Q is the rate of heat transfer (in watts or joules per second),
- k is the thermal conductivity of the material (for copper, k≈398W/m⋅K),
- A is the cross-sectional area (in square meters),
- TH is the temperature at the hot end (in °C),
- TC is the temperature at the cold end (in °C),
- L is the thickness of the slab (in meters).
1. Convert the given values to SI units:
- Length L=15.0cm=0.15m
- Area A=105cm2=105×10−4m2=0.0105m2
- Temperature at hot end TH=125°C
- Temperature at cold end TC=10.0°C
2. Calculate the temperature difference:
TH−TC=125−10=115°C
3. Substitute the values into Fourier's law:
Q=398W/m⋅K⋅0.0105m2⋅115K0.15m
4. Calculate the numerator:
398⋅0.0105⋅115=398⋅1.2075=480.045W
5. Calculate the conduction rate:
Q=480.0450.15=3200.3W
6. Convert to kilojoules per second (kW):
Q≈3.2kW
Final Answer:
The conduction rate through the slab is approximately 3.2 kW.
---
- Q is the rate of heat transfer (in watts or joules per second),
- k is the thermal conductivity of the material (for copper, k≈398W/m⋅K),
- A is the cross-sectional area (in square meters),
- TH is the temperature at the hot end (in °C),
- TC is the temperature at the cold end (in °C),
- L is the thickness of the slab (in meters).
- Length L=15.0cm=0.15m
- Area A=105cm2=105×10−4m2=0.0105m2
- Temperature at hot end TH=125°C
- Temperature at cold end TC=10.0°C
TH−TC=125−10=115°C
Q=398W/m⋅K⋅0.0105m2⋅115K0.15m
398⋅0.0105⋅115=398⋅1.2075=480.045W
Q=480.0450.15=3200.3W
Q≈3.2kW
The conduction rate through the slab is approximately 3.2 kW.
Topper's Solved these Questions
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS
60 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE )
8 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - CHECKPOINT 2
1 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
Similar Questions
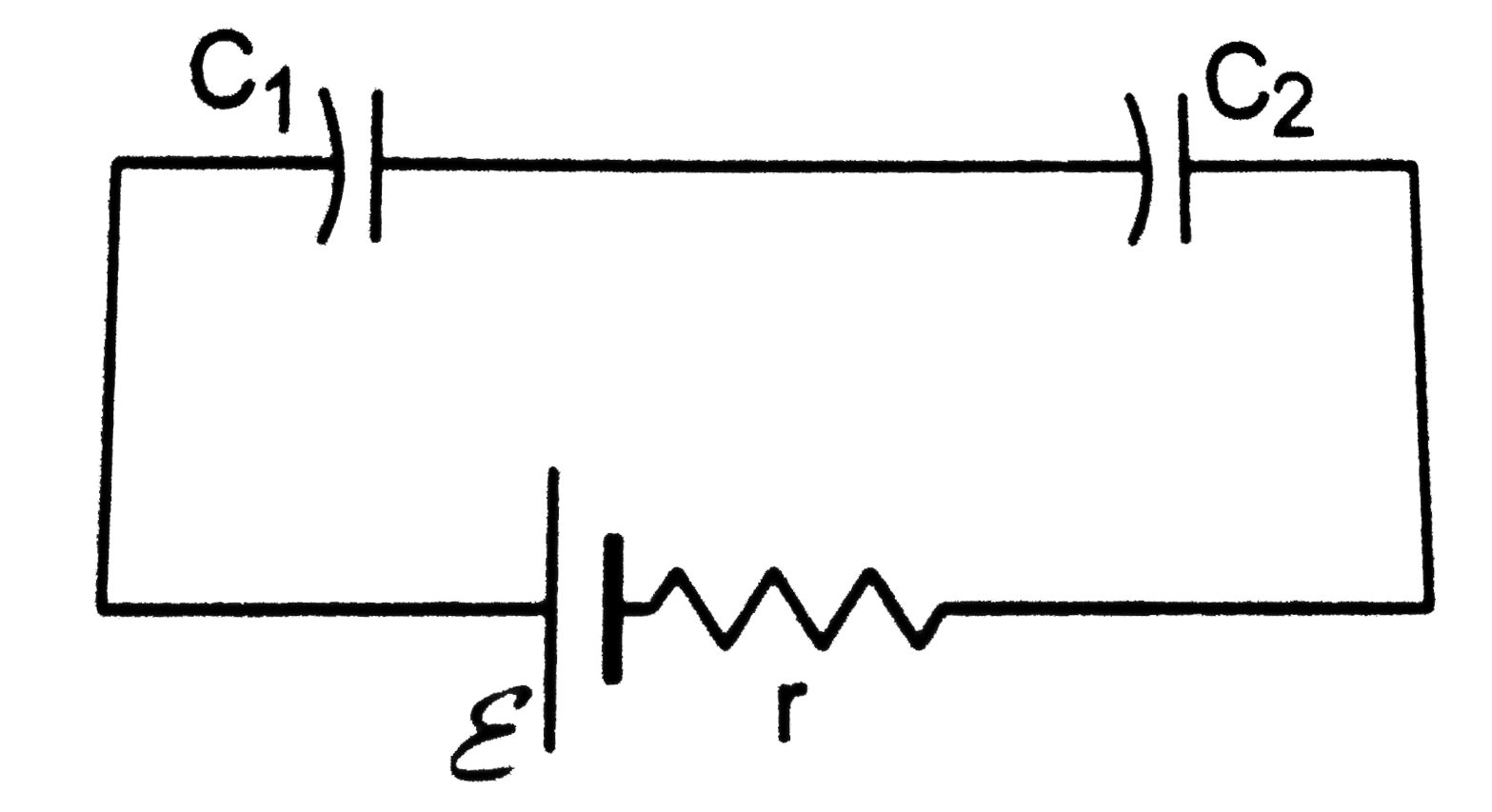
Consider the situation shown in figure.The switch is closed at t=0when the capacitor C1as a function of time t.
View SolutionFigure shows ( in cross section ) a wall consisting of four layers, with thermal conductivities k1=0.060W/m.K,k3=0.040W/m.K, and k4=0.12W/m.K(k2 is not known). The layer thickness are L1=1.2cm,L3=5.6cm, and L4=4.0cm (L2 is not known ) . The known temperatures are T1=30∘C,T12=25∘C, and T4=−10∘C . Energy transfer through the wall is steady. What is interface temperature T34 ?

View Solution
Knowledge Check
Consider the circuit shown in the figure. Find the charge on capacitor C between A and D in steady state.
 ACεBCε/2CCε/3Dzero
ACεBCε/2CCε/3DzeroSix identical uniform conducting rods are fixed to make a regular hexagon as shown. The ends A and C are maintained at constant temperature 2T0 and 6T0. After the steady state is reached. Pick up the correct relation between temperatures TB,TB,TE and TF of ends B,D,E and F respectively.
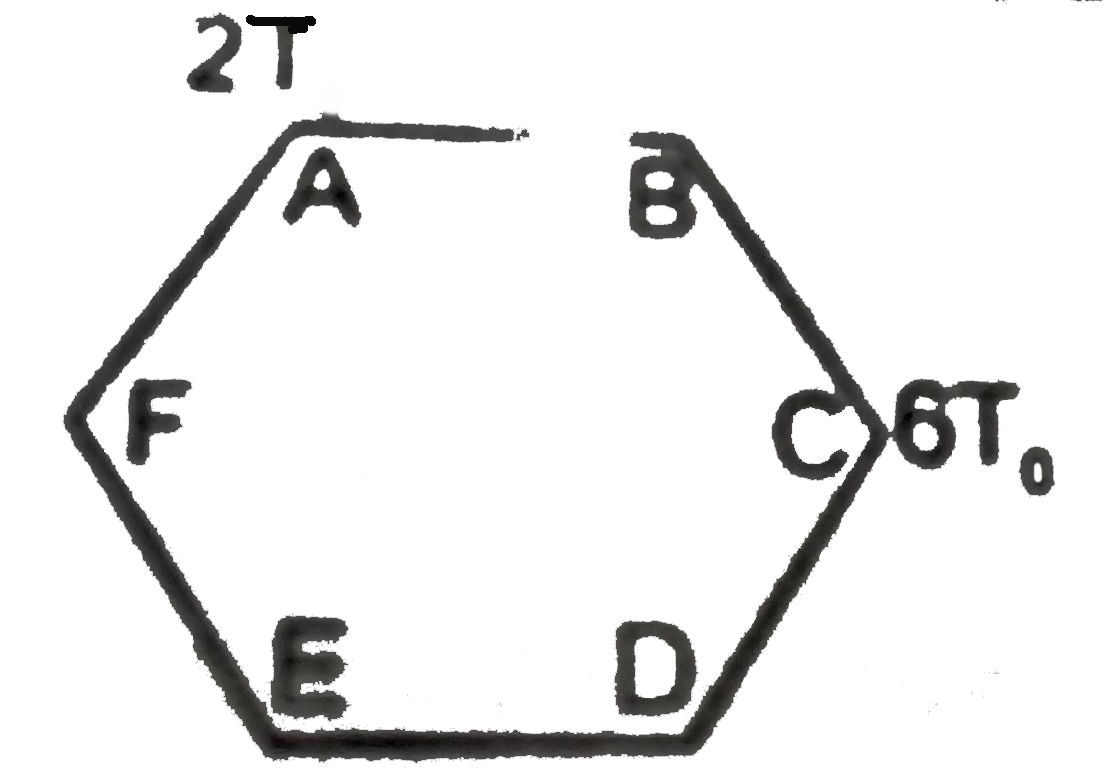 ATD>TE=TB>TFBTD=TB>TE>TFCTD>TE>TF=TBDTB>TF=TE>TD
ATD>TE=TB>TFBTD=TB>TE>TFCTD>TE>TF=TBDTB>TF=TE>TD
Three rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View SolutionWhat is the temperature of the steel-copper junction in the steady state system show in Fig. 7(e).17? Length of steel rod = 15.0 cm, length of the copper rod = 10.0 cm, temperature of the furnace =300∘C, temperature of other end 0∘C. The are of cross-section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel =50.2js−1m−1K−1 and of copper =3895js−1m−1K−1).

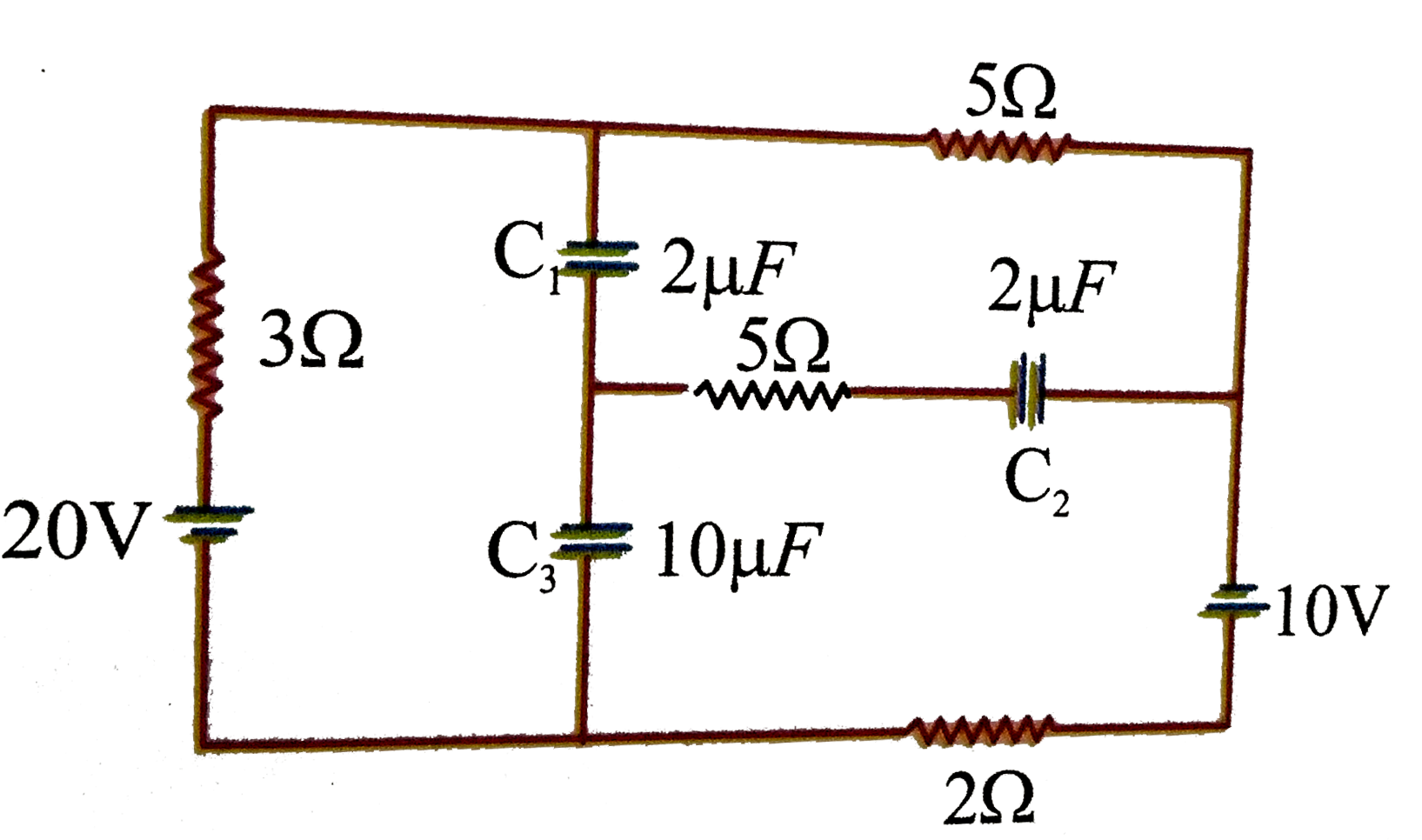
View SolutionIn the circuit shown in figure. The charge on capacitor C2 in steady state is 10xμC. Find the value of x.
 .
.
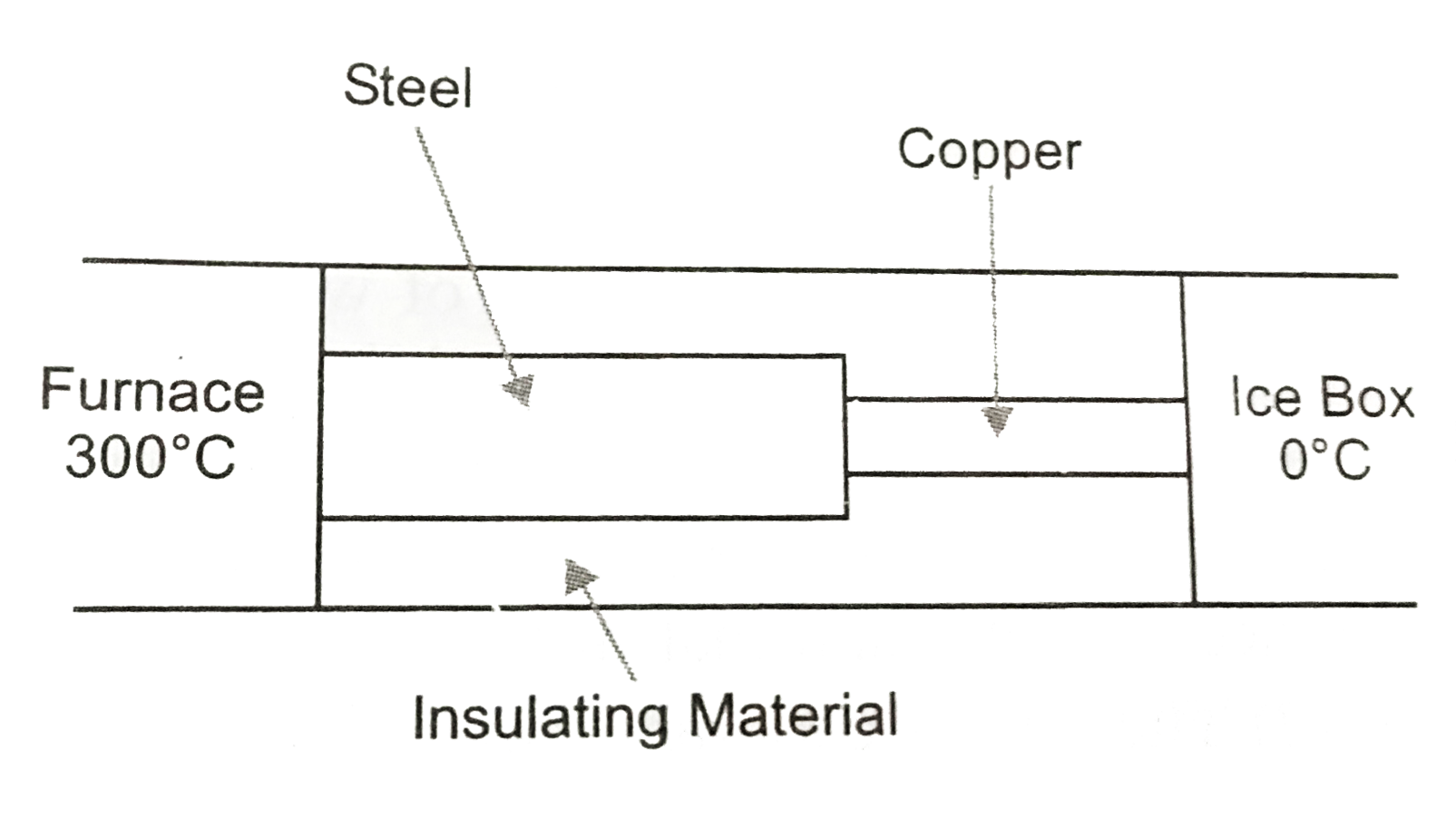
View SolutionWhat is the temperature of steel-copper jumction in the steady state of the system shown in fig. Length of the steel rod = 30.0 cm, length of the copper rod = 20.0 cm, temperature of the furnace = 300∘C, temperature of cold end =0∘C . The area of cross-section of the steel rod is twice that of the copper rod. thermal conductivity of steel = 50.2Js−1m−1.∘C−1 and of copper = 358Js−1m−1.∘C−1.
View SolutionHeat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View SolutionFigure shows the cross section of a wall made of white pine of thickness La and brick of thickness Ld==2.0La , sandwiching two layers of unknonw material with identical thicknesses and thermal conductivities. The thermal conductivity of the pine is ka and that of the brick is kd(=5.0ka). The face area A of the wall is unknown. Thermal conduction through the wall has reached the steady state, the only known interface temperatures are T1=25∘C,T2=20∘C, and T5=−10∘C. What is interface temperature T4 ?
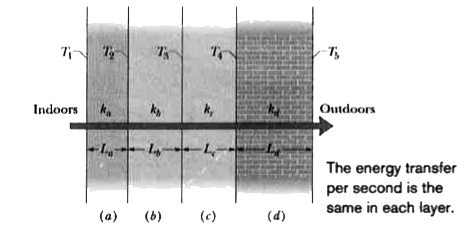
View Solution
