At t=0, the displacement x(0) of the block in a linear oscillator like that of Fig . 15.5 is −8.50cm. (Read x(0) as ''x at time zero'') The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What is the angular frequency ω of this system?
To find the angular frequency ω of the linear oscillator given the initial conditions, we can follow these steps:
Step 1: Write down the equations for displacement, velocity, and acceleration
For a simple harmonic oscillator, the displacement x(t), velocity v(t), and acceleration a(t) can be expressed as:
1. x(t)=Asin(ωt+ϕ)
2. v(t)=Aωcos(ωt+ϕ)
3. a(t)=−Aω2sin(ωt+ϕ)
Where:
- A is the amplitude
- ϕ is the phase constant
- ω is the angular frequency
Step 2: Substitute the initial conditions at t=0
At t=0:
- Displacement x(0)=−8.50cm=−0.0850m
- Velocity v(0)=−0.920m/s
- Acceleration a(0)=+47.0m/s2
Substituting these values into the equations gives us:
1. −0.0850=Asin(ϕ) (Equation 1)
2. −0.920=Aωcos(ϕ) (Equation 2)
3. 47.0=−Aω2sin(ϕ) (Equation 3)
Step 3: Solve for ω
From Equation 1, we can express Asin(ϕ):
Asin(ϕ)=−0.0850
From Equation 3, we can express Aω2sin(ϕ):
Aω2sin(ϕ)=−47.0
Now, we can divide Equation 3 by Equation 2:
Aω2sin(ϕ)Aωcos(ϕ)=−47.0−0.920
This simplifies to:
ωsin(ϕ)cos(ϕ)=47.00.920
Thus:
ωtan(ϕ)=47.00.920
Step 4: Find ω using the relationship between acceleration and displacement
From Equation 3, we can rearrange it to find ω2:
ω2=−a(0)Asin(ϕ)
Substituting a(0)=47.0m/s2 and Asin(ϕ)=−0.0850:
ω2=47.00.0850
Calculating this gives:
ω2=552.94s−2
Taking the square root:
ω=√552.94≈23.5rad/s
Final Answer
The angular frequency ω of the system is approximately 23.5rad/s.
---
For a simple harmonic oscillator, the displacement x(t), velocity v(t), and acceleration a(t) can be expressed as:
1. x(t)=Asin(ωt+ϕ)
2. v(t)=Aωcos(ωt+ϕ)
3. a(t)=−Aω2sin(ωt+ϕ)
- A is the amplitude
- ϕ is the phase constant
- ω is the angular frequency
At t=0:
- Displacement x(0)=−8.50cm=−0.0850m
- Velocity v(0)=−0.920m/s
- Acceleration a(0)=+47.0m/s2
1. −0.0850=Asin(ϕ) (Equation 1)
2. −0.920=Aωcos(ϕ) (Equation 2)
3. 47.0=−Aω2sin(ϕ) (Equation 3)
From Equation 1, we can express Asin(ϕ):
Asin(ϕ)=−0.0850
Aω2sin(ϕ)=−47.0
Aω2sin(ϕ)Aωcos(ϕ)=−47.0−0.920
This simplifies to:
ωsin(ϕ)cos(ϕ)=47.00.920
Thus:
ωtan(ϕ)=47.00.920
From Equation 3, we can rearrange it to find ω2:
ω2=−a(0)Asin(ϕ)
Substituting a(0)=47.0m/s2 and Asin(ϕ)=−0.0850:
ω2=47.00.0850
Calculating this gives:
ω2=552.94s−2
Taking the square root:
ω=√552.94≈23.5rad/s
The angular frequency ω of the system is approximately 23.5rad/s.
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint
8 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems
39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
At t=0, the displacement x(0) of the block in a linear oscillator like that of Fig. 15.5 is −8.50cm. (Read x(0) as ''x at time zero''). The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What is the phase constant ϕ and amplitude xm ?
View SolutionAt t=0, the displacement x(0) of the block in a linear oscillator like that of Fig . 15.5 is −8.50cm. (Read x(0) as ''x at time zero'') The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What are the phase constant ϕ and amplitude xm?
View Solution
Knowledge Check
If at some instant of time, the displacement of a simple harmonic oscillator is 0.02 m and its acceleration is 2ms−2, then the angular frequency of the oscillator is
A100 rad s−1B10 rad s−1C1 rad s−1D0.1 rad s−1If the displacement of simple pendulum at any time is 0.02 m and acceleration is 2m/s2, then in this time angular velocity will be
A100 rad/sB10 rad/sC1 rad/sD0.1 rad/sIf a simple harmonic oscillator has got a displacement of 0.02 m and acceleration equal to 0.02m/s2 at any time, the angular frequency of the oscillator is equal to:
A10 rad/sB0.1 rad/sC100 rad/sD1 rad/s
If the position of the block in a block-spring oscillator is given by
x(t)=(3.00×10−3m)cos[(4.00rad/s)t+0.120rad], what is the block's position, velocity and acceleration at time t= 2.30s?
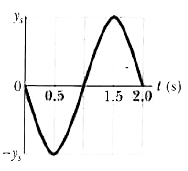
View SolutionFor a particular transverse standing wave on a long string, one of the antinodes is at r=0 and an adjacent node is at x=0.10 m. The displacement y(t) of the string particle at x =0 is shown in Fig. 16-40, where the scale of the y axis is set by ys=4.0cm. When t = 0.50 s, what is the displacement of the string particle at (a) x= 0.20 m and (b) x= 0.30 m? What is the transverse velocity of the string particle at x =0.20 m at (c) t=0.50s and (d) t=1.0s? (e) Sketch the standing wave at t=0.50s for the range x=0 to x=0.40m.
View SolutionA body oscillates with a simple harmonic motion having amplitude 0.05 m. At a certain instant of time, its displacement is 0.01 m and acceleration is 1.0m/s2. The period of oscillation is
View SolutionIf the displacement of simple pendulum at any time is 0.02 m and acceleration is 2m/s2,then in this time angular velocity will be
View SolutionFor a simple harmonic oscillator, the aceeleration is 3m/s2 when the displacement is 0.03 m. The angular frequency of the oscillator is
View Solution
