If the position of the block in a block-spring oscillator is given by
x(t)=(3.00×10−3m)cos[(4.00rad/s)t+0.120rad], what is the block's position, velocity and acceleration at time t= 2.30s?
To solve the problem, we need to find the position, velocity, and acceleration of a block in a block-spring oscillator at a specific time t=2.30s. The position of the block is given by the equation:
x(t)=(3.00×10−3m)cos((4.00rad/s)t+0.120rad)
Step 1: Calculate the Position at t=2.30s
Substituting t=2.30s into the position equation:
x(2.30)=(3.00×10−3m)cos((4.00rad/s)×(2.30s)+0.120rad)
Calculating the argument of the cosine:
(4.00×2.30)+0.120=9.20+0.120=9.32rad
Now, calculate the cosine:
x(2.30)=(3.00×10−3)cos(9.32)
Using a calculator to find cos(9.32):
cos(9.32)≈−0.005
Now, substituting back into the position equation:
x(2.30)≈(3.00×10−3)×(−0.005)≈−0.000015m≈−0.0029m
Step 2: Calculate the Velocity
The velocity v(t) is the derivative of the position function x(t):
v(t)=dxdt=−(3.00×10−3m)(4.00rad/s)sin((4.00rad/s)t+0.120rad)
Substituting t=2.30s:
v(2.30)=−(3.00×10−3)(4.00)sin(9.32)
Calculating sin(9.32):
sin(9.32)≈−0.999
Now substituting back into the velocity equation:
v(2.30)≈−(3.00×10−3)(4.00)(−0.999)≈0.012m/s
Step 3: Calculate the Acceleration
The acceleration a(t) is the derivative of the velocity function v(t):
a(t)=dvdt=−(3.00×10−3)(4.00)2cos((4.00rad/s)t+0.120rad)
Substituting t=2.30s:
a(2.30)=−(3.00×10−3)(16)cos(9.32)
Using the previously calculated value of cos(9.32):
a(2.30)≈−(3.00×10−3)(16)(−0.005)≈0.00024m/s2
Final Results
- Position x(2.30)≈−0.0029m
- Velocity v(2.30)≈0.012m/s
- Acceleration a(2.30)≈0.00024m/s2
- Velocity v(2.30)≈0.012m/s
- Acceleration a(2.30)≈0.00024m/s2
Topper's Solved these Questions
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Checkpoint
Explore 8 Videos
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Problems
Explore 39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:RESNICK AND HALLIDAYChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:PRACTICE QUESTIONS (MATRIX-MATCH)
Explore 10 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS(Integer Type)
Explore 4 Videos
Similar Questions
The position of a particle moving along an x axis is given by x=12t2−2t3, where x is in meters and t is in seconds. Determine (a) the position, (b) the velocity, and (c) the acceleration of the particle at t=3.5s. (d) What is the maximum positive coordinate reached by the particle and (e) at what time is it reached ? (f) What is the maximum positive velocity reached by the particle and (g) at what time is it reached ? (h) What is the acceleration of the particle at the instant the particle is not moving ( other than at t=0 ) ? (i) Determine the average velocity of the particle between t=0 and t=3s .
View SolutionIf the phase angle for a block -spring system in SHM is π/8 rad and the block's position is given by x=xmcos(ωt+ϕ), what is the ratio of the kinetic energy to the potential energy at time t= 0?
View Solution
Knowledge Check
A 0.10 kg block oscillates back and forth along a horizontal surface. Its displacement from the origin is given by: x=(10cm)cos[(10rads)t+π/2rad] what is the maximum acceleration experiences by the block
A10m/s2B10πm/s2C10π2m/s2D10π3m/s2The position of a body with respect to time is given by x=4t3–6t2+20t+12 . Acceleration at t = 0 will be-
A−12 unitsB12 unitsC24 unitsD−24 unitsThe friction force acting on the block at time t=4s will be
 A50NB30NC25NDNone
A50NB30NC25NDNone
Figure is a graph of the coordinate of a spider crawling along the x-axis. (a) Fraph tis velocity and acceleration as functionsof time. (b) In a motion diagram, show the position, velocity, and acceleration of the spider at the five times: t=2.5s, t=10 s, t=20 s, t=30 s,
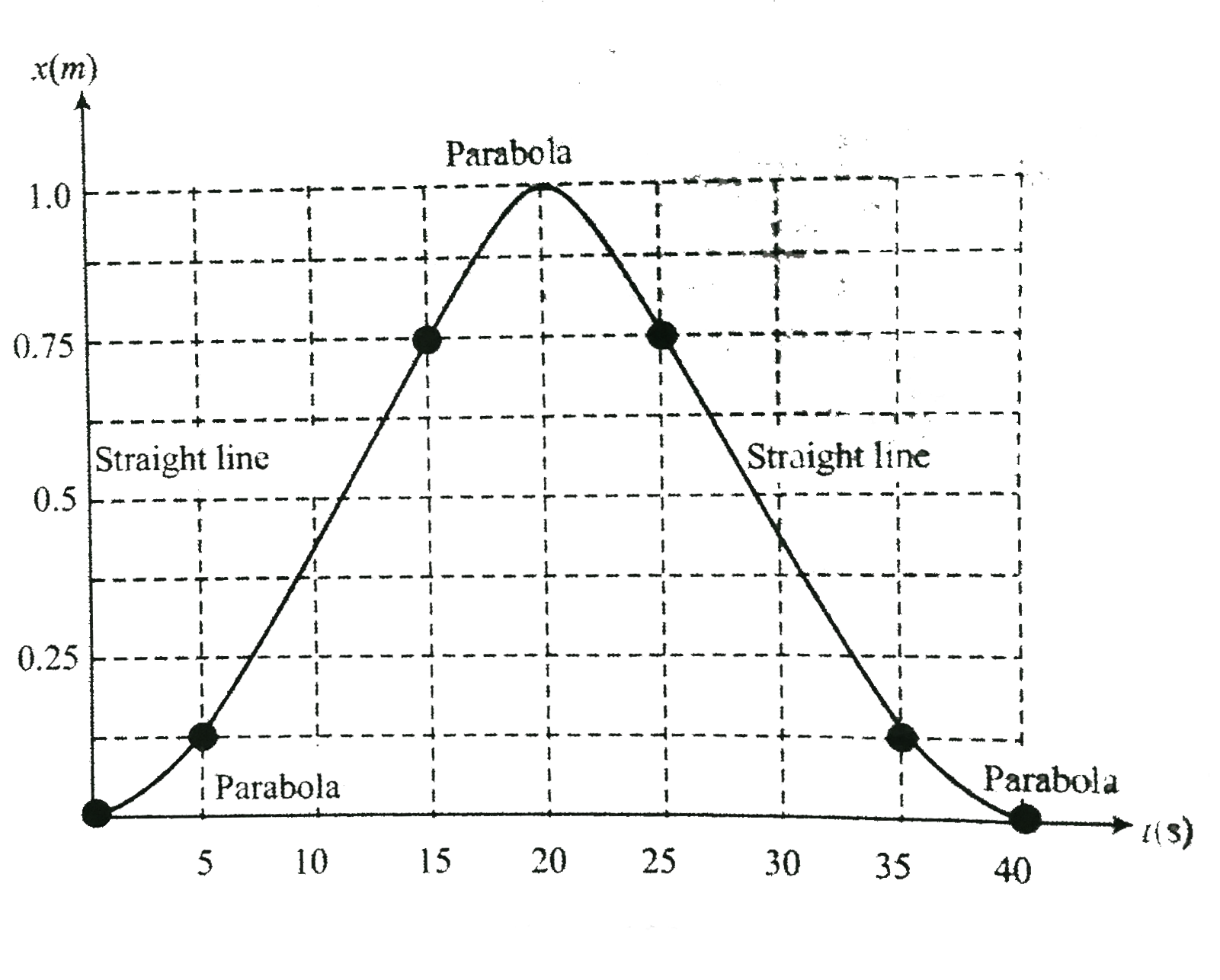 .
.
View SolutionThe position of a particle moving along the x axis is given in centimeters by x=9.75+1.50t3, where t is in seconds. Calculate (a) the average velocity during the time interval t=2.00s to t=3.00s, (b) the instantaneous velocity at t=2.00s , (c) the instantaneous velocity at t=3.00s, (d) the instantaneous velocity at t=2.50s, and (e) the instantaneous velocity when the particle is midway between its positions at t=2.00s and t=3.00s . (f) Graph x versus t and indicate your answers graphically
View SolutionOne end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m=1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x=10+3sin(10t). Here, t is in second and x in cm. Another block of mass M=3kg, moving towards the origin with velocity 30cm/s collides with the block performing SHM at t=0 and gets stuck to it. Calculate

(a) new amplitude of oscillations,
(b) neweqution for position of the combined body,
( c) loss of energy during collision. Neglect friction.
View SolutionAn oscillator consists of a block attached to a spring of spring constant K=300 N/m. At some time t the position (measured from its equilibrium position), velocity and acceleration of the block are
x=0.1m,v=−15m/s and a=−90m/s2. What is the ampliof motion and the mass of the block ?
View SolutionThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The distance travelled by body in time interval t = 0 to t = 3 s is
View Solution

